5: 固有値と固有ベクトル

\[ A = \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix}, \] このとき \[ A\begin{pmatrix} 1 \cr 0 \end{pmatrix} = \begin{pmatrix} 1\cr 3 \end{pmatrix},\quad A\begin{pmatrix} 0\cr 1 \end{pmatrix} = \begin{pmatrix} 2\cr 4 \end{pmatrix}. \]

• 従って, 例えば \[ \begin{array}{rl} A\begin{pmatrix} 3\cr 5 \end{pmatrix} &= 3A\begin{pmatrix} 1\cr 0 \end{pmatrix} + 5A\begin{pmatrix} 0\cr 1 \end{pmatrix} \cr &= 3\begin{pmatrix} 1\cr 3 \end{pmatrix} + 5\begin{pmatrix} 2\cr 4 \end{pmatrix} \cr &= \begin{pmatrix} 13\cr 29 \end{pmatrix}. \end{array} \]

\[ A = \begin{pmatrix} 1&1/2\cr 1/2&1 \end{pmatrix},\quad \mathbf{v} = \begin{pmatrix} a\cr b \end{pmatrix}\in\mathbb{R}^2. \]

• このとき, \[ A\mathbf{v} = \begin{pmatrix}a+b/2\cr a/2+b\end{pmatrix}\in\mathbb{R}^2 \] となる.
• つまり, ベクトル $\mathbf{v}\in\mathbb{R}^2$ に左から行列 $A$ を掛けることで, ベクトル $\mathbf{v}$ で表される $xy$ 平面上の矢印 (もしくは点) は, $A\mathbf{v}$ で表される矢印 (もしくは点) に変換される.

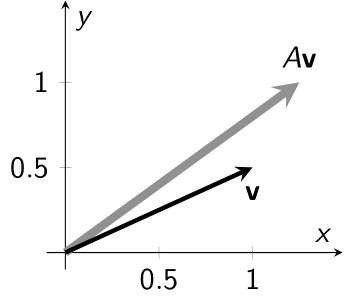
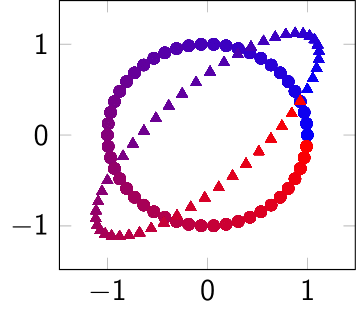
$1$ つ目の図は, ベクトル $\mathbf{v}\in\mathbb{R}^2$ を矢印で表現し, 対応する $A\mathbf{v}$ もやはり矢印で表したものである. $2$ つ目の図は, 半径 $1$ の円周上にある $\mathbf{v}\in\mathbb{R}^2$ を丸で, 対応する $A\mathbf{v}$ を三角でプロットしたものである.

\[ A = \begin{pmatrix} 1&1/2\cr 1/2&1 \end{pmatrix}. \]

• 例えば $\mathbf{v}_1 = \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1\cr -1 \end{pmatrix}$ とすると, $A\mathbf{v}_1 = \dfrac{1}{2}\mathbf{v}_1$ となるため $\mathbf{v}_1$ は固有ベクトルであり, 対応する固有値は $1/2$ である.
• 例えば $\mathbf{v}_2 = \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1\cr 1 \end{pmatrix}$ とすると, $A\mathbf{v}_2 = \dfrac{3}{2}\mathbf{v}_2$ となるため $\mathbf{v}_2$ は固有ベクトルであり, 対応する固有値は $3/2$ である.
• なお, $\mathbf{v}_1$, $\mathbf{v}_2$ に $1/\sqrt{2}$ が含まれるのは, ベクトルの大きさを $1$ に揃えるためである (ベクトルの大きさに興味がないならば不要である).

ここで, 固有ベクトルを図示するとどのようになるか見てみよう.

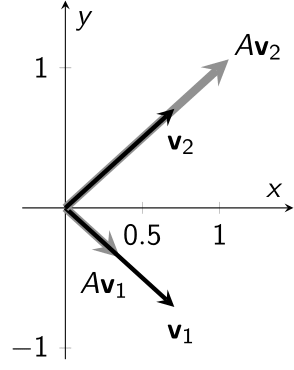
図は例に挙げた行列 $A$ の固有ベクトル $\mathbf{v}_1$, $\mathbf{v}_2$ と, $A\mathbf{v}_1$ および $A\mathbf{v}_2$ を示したものである. このように, 行列 $A$ の固有ベクトルは $A$ による変換で向きを変えないベクトルであり, 対応する固有値 $\lambda_1$, $\lambda_2$ は固有ベクトルに対する $A$ による変換の拡大率と解釈することができる.

実際に, 大きさ $1$ の固有ベクトル $\mathbf{v}_1$ に対し, $A\mathbf{v}_1 = \dfrac{1}{2}\mathbf{v}_1$ であるため, $A\mathbf{v}_1$ は大きさが $1/2$ であり, 向きは $\mathbf{v}_1$ と同じ矢印として図示される.

\[ A = \begin{pmatrix} \cos\alpha & -\sin\alpha\cr \sin\alpha & \cos\alpha \end{pmatrix}. \]

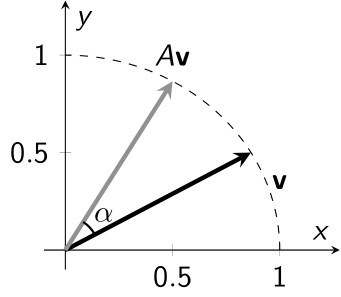
• いま, ベクトル $\mathbf{v} = \begin{pmatrix} a \cr b \end{pmatrix}$ の極座標表示が \[ \mathbf{v} = \begin{pmatrix} r\cos\theta\cr r\sin\theta \end{pmatrix} \] と与えられていたとする. このとき, 三角関数の加法定理より \[ \begin{array}{rl} A\mathbf{v} &= \begin{pmatrix} \cos\alpha & -\sin\alpha\cr \sin\alpha & \cos\alpha \end{pmatrix}\begin{pmatrix} r\cos\theta\cr r\sin\theta \end{pmatrix} \cr &= \begin{pmatrix} r(\cos\theta\cos\alpha-\sin\theta\sin\alpha)\cr r(\sin\theta\cos\alpha + \cos\theta\sin\alpha) \end{pmatrix} \cr &= \begin{pmatrix} r\cos(\theta+\alpha)\cr r\sin(\theta+\alpha) \end{pmatrix} \end{array} \] が得られる. つまり, この行列 $A$ はベクトル $\mathbf{v}$ を $\alpha$ だけ回転する変換を表している.
• このような行列 $A$ を回転行列と呼ぶ.
• いま, $\alpha\neq n\pi$ とする. このとき, 行列 $A$ は実数の固有値を持たない (ベクトル $\mathbf{v}$ は行列 $A$ により回転してしまうため, $\mathbf{v}$ と $A\mathbf{v}$ の向きが一致することはない).
• (実は, 複素数まで認めればこの行列の固有値と固有ベクトルは存在する)

\[ A = \begin{pmatrix} 1&1/2\cr 1/2&1 \end{pmatrix}. \]

• 特性多項式は \[ \begin{array}{rl} \det(\lambda I-A) &= \lambda^2 - 2\lambda + 3/4 \cr &= (\lambda-1/2)(\lambda-3/2). \end{array} \]
• 従って \[ \det(\lambda I-A)=0\iff \lambda = 1/2,\ 3/2 \] となり, \[ \lambda_1 = 1/2,\quad \lambda_2 = 3/2 \] が行列 $A$ の固有値となる.
• ここで, \[ (\lambda_1I-A)\mathbf{v}_1 = \begin{pmatrix} -1/2 & -1/2\cr -1/2&-1/2 \end{pmatrix}\mathbf{v}_1= \mathbf{0} \] を考えると, 例えば $\mathbf{v}_1 = \begin{pmatrix} 1\cr -1 \end{pmatrix}$ はこれを満たすため, その任意の複素数倍が固有値 $\lambda_1=1/2$ に対応する固有ベクトルである: \[ \mathbf{v}_1 = c_1 \begin{pmatrix} 1\cr -1 \end{pmatrix},\quad c_1\neq0 \text{は任意}. \]
• 同様に, \[ (\lambda_2I-A)\mathbf{v}_2 = \begin{pmatrix} 1/2 & -1/2\cr -1/2&1/2 \end{pmatrix}\mathbf{v}_2= \mathbf{0} \] を考えると, 例えば $\mathbf{v}_2 = \begin{pmatrix} 1\cr 1 \end{pmatrix}$ はこれを満たすため, その任意の複素数倍が固有値 $\lambda_2=3/2$ に対応する固有ベクトルである: \[ \mathbf{v}_2 = c_2\begin{pmatrix} 1\cr 1 \end{pmatrix},\quad c_2\neq0 \text{は任意.} \]

\[ A = \begin{pmatrix} \cos\alpha & -\sin\alpha\cr \sin\alpha & \cos\alpha \end{pmatrix} \qquad (\alpha\neq n\pi). \]

• 特性多項式は \[ \det(\lambda I-A) = \lambda^2 - 2\lambda\cos\alpha + 1. \]
• 従って ($2$ 次方程式の解の公式を用いて) \[ \begin{array}{rl} \det(\lambda I-A)=0\iff \lambda &= \cos\alpha \pm \sqrt{\cos^2\alpha - 1} \cr &= \cos\alpha \pm i \sin\alpha \end{array} \] となり, \[ \lambda_1 = \cos\alpha+i\sin\alpha, \] \[ \lambda_2 = \cos\alpha-i\sin\alpha \] が行列 $A$ の固有値となる, ただし $i=\sqrt{-1}$ は虚数単位.
• ここで, \[ (\lambda_1I-A)\mathbf{v}_1 = \begin{pmatrix} i\sin\alpha & \sin\alpha\cr -\sin\alpha & i\sin\alpha \end{pmatrix}\mathbf{v}_1= \mathbf{0} \] を考えると, 例えば $\mathbf{v}_1 = \begin{pmatrix} 1\cr -i \end{pmatrix}$ はこれを満たすため, その任意の複素数倍が対応する固有ベクトルである: \[ \mathbf{v}_1 = c_1\begin{pmatrix} 1\cr -i \end{pmatrix},\quad c_1\neq0 \text{は任意.} \]
• 同様に, \[ (\lambda_2I-A)\mathbf{v}_2 = \begin{pmatrix} -i\sin\alpha & \sin\alpha\cr -\sin\alpha & -i\sin\alpha \end{pmatrix}\mathbf{v}_2= \mathbf{0} \] を考えると, 例えば $\mathbf{v}_2 = \begin{pmatrix} 1\cr i \end{pmatrix}$ はこれを満たすため, その任意の複素数倍が対応する固有ベクトルである: \[ \mathbf{v}_2 = c_2\begin{pmatrix} 1\cr i \end{pmatrix},\quad c_2\neq0 \text{は任意.} \]

\[ A = \begin{pmatrix} 1&1\cr 0&1 \end{pmatrix}. \]

• 特性多項式は \[ \det(\lambda I-A) = (\lambda-1)^2. \]
• 従って \[ \det(\lambda I-A)=0\iff \lambda = 1 \] となり, 固有値は $\lambda_1= 1$ のみ.
• ここで, \[ (\lambda_1I-A)\mathbf{v}_1 = \begin{pmatrix} 0& -1\cr 0 & 0 \end{pmatrix}\mathbf{v}_1= \mathbf{0} \] を考えると, 例えば $\mathbf{v}_1 = \begin{pmatrix} 1\cr 0 \end{pmatrix}$ はこれを満たすため, その任意の複素数倍が対応する固有ベクトルである: \[ \mathbf{v}_1 = c_1 \begin{pmatrix} 1\cr 0 \end{pmatrix},\quad c_1\neq0 \text{は任意.} \]

\[ A = \begin{pmatrix} 1&1/2\cr 1/2&1 \end{pmatrix}. \]

• 固有値は $\lambda_1 = 1/2$ と $\lambda_2 = 3/2$ であり, 対応する固有ベクトルは, 例えば \[ \mathbf{v}_1 = \begin{pmatrix} 1\cr -1 \end{pmatrix},\quad \mathbf{v}_2 = \begin{pmatrix} 1\cr 1 \end{pmatrix} \] であった.
• これを用いて, \[ P = \begin{pmatrix} \mathbf{v}_1, \mathbf{v}_2 \end{pmatrix} = \begin{pmatrix} 1&1\cr -1&1 \end{pmatrix} \] とすると, \[ P^{-1}AP = \begin{pmatrix} \lambda_1&0\cr 0&\lambda_2 \end{pmatrix} = \begin{pmatrix} 1/2 & 0 \cr 0 & 3/2 \end{pmatrix} \] が得られる. 実際, \[ \begin{array}{rl} AP &= \begin{pmatrix} 1/2&3/2\cr -1/2&3/2 \end{pmatrix} \cr &= \begin{pmatrix} 1&1\cr -1&1 \end{pmatrix}\begin{pmatrix} 1/2&0\cr 0&3/2 \end{pmatrix} \cr &= P\begin{pmatrix} 1/2&0\cr 0&3/2 \end{pmatrix} \end{array} \] を確かめることができる.
• 対角化が固有ベクトルの大きさに依存しない (固有ベクトルの向きにのみ依存する) ことを確かめてみる. 例えば, 対応する固有ベクトルを \[ \mathbf{v}_1 = \begin{pmatrix} 2\cr -2 \end{pmatrix},\quad \mathbf{v}_2 = \begin{pmatrix} 1/2\cr 1/2 \end{pmatrix} \] としたときには, \[ P = \begin{pmatrix} 2&1/2\cr -2&1/2 \end{pmatrix} \] となり, \[ \begin{array}{rl} AP &= \begin{pmatrix} 1&3/4\cr -1&3/4 \end{pmatrix} \cr &= \begin{pmatrix} 2&1/2\cr -2&1/2 \end{pmatrix}\begin{pmatrix} 1/2&0\cr 0&3/2 \end{pmatrix} \cr &= P\begin{pmatrix} 1/2 & 0\cr 0&3/2 \end{pmatrix} \end{array} \] より \[ P^{-1}AP = \begin{pmatrix} 1/2 & 0 \cr 0 & 3/2 \end{pmatrix} = \begin{pmatrix} \lambda_1 & 0 \cr 0 & \lambda_2 \end{pmatrix} \] と, 対角化の結果が先ほどと一致する.
• 固有値 $\lambda_1$ と $\lambda_2$ (および対応する固有ベクトル $\mathbf{v}_1$ と $\mathbf{v}_2$) の順序は入れ替えても良い. 例えば $\lambda_1 = 3/2$, $\lambda_2 = 1/2$, 対応する固有ベクトルを \[ \mathbf{v}_1 = \begin{pmatrix} 1 \cr 1 \end{pmatrix},\quad \mathbf{v}_2 = \begin{pmatrix} 1 \cr -1 \end{pmatrix} \] としたときは, \[ P = \begin{pmatrix} \mathbf{v}_1, \mathbf{v}_2 \end{pmatrix} = \begin{pmatrix} 1 & 1 \cr 1 & -1 \end{pmatrix} \] について, \[ \begin{array}{rl} AP &= \begin{pmatrix} 3/2 & 1/2 \cr 3/2 & -1/2 \end{pmatrix} \cr &= \begin{pmatrix} 1 & 1 \cr 1 & -1 \end{pmatrix}\begin{pmatrix} 3/2 & 0 \cr 0 & 1/2 \end{pmatrix} \cr &= P\begin{pmatrix} 3/2 & 0 \cr 0 & 1/2 \end{pmatrix} \end{array} \] より \[ P^{-1}AP = \begin{pmatrix} 3/2 & 0 \cr 0 & 1/2 \end{pmatrix} \] が得られる. 上の結果と固有値の順序が異なっているものの, いずれにしても固有値を対角成分に持つ対角行列と相似であることが確認できる.

\[ A = \begin{pmatrix} 1&1/2\cr 1/2&1 \end{pmatrix}. \] いま, $A^k$ を対角化を用いて計算してみよう. 行列 $A$ の固有値は $\lambda_1 = 1/2$ と $\lambda_2 = 3/2$ であり, 対応する固有ベクトルは, 例えば \[ \mathbf{v}_1 = \begin{pmatrix} 1\cr -1 \end{pmatrix},\quad \mathbf{v}_2 = \begin{pmatrix} 1\cr 1 \end{pmatrix} \] であった. そこで, \[ P = \begin{pmatrix} 1&1\cr -1&1 \end{pmatrix},\quad P^{-1} = \begin{pmatrix} 1/2 & -1/2\cr 1/2&1/2 \end{pmatrix} \] とおくと, \[ \begin{array}{rl} A^k &= P(P^{-1}AP)^kP^{-1} \cr &= P\begin{pmatrix} \lambda_1 & 0 \cr 0 & \lambda_2 \end{pmatrix}^k P^{-1} \cr &= P\begin{pmatrix} \lambda_1^k&0\cr 0&\lambda_2^k \end{pmatrix}P^{-1} \cr &= \dfrac{1}{2}\begin{pmatrix} \lambda_1^k+\lambda_2^k & -\lambda_1^k+\lambda_2^k\cr -\lambda_1^k+\lambda_2^k& \lambda_1^k+\lambda_2^k \end{pmatrix} \cr &= \dfrac{1}{2^{k+1}}\begin{pmatrix} 1+3^k & -1+3^k \cr -1+3^k & 1+3^k \end{pmatrix} \end{array} \] と計算することができる.