3: 行列式

3.1: 逆行列の存在

ここでは, 行列 $A$ として常に正方行列を考えることにする. この行列 $A$ の逆行列について, ここまでの内容を以下にいくつか再掲する:

正方行列 $A$ に対して, 同じ型の正方行列 $B$ であって \[ AB = BA = I \] を満たすものが存在するならば, $B$ を $A$ の逆行列 (inverse matrix) といい, $A^{-1}$ と表記する. 正方行列 $A$ の逆行列が存在するならば, $A$ を正則行列 (regular matrix) もしくは可逆行列 (invertible matrix) という.

逆行列について以下が成立する:

$A^{-1}$ が存在するならば, $(A^{-1})^{-1} = A$.
$A^{-1}$ は存在するならばただ$1$つに定まる.
同じ型の正方行列 $A$, $B$ に対し, $A^{-1}$, $B^{-1}$ が存在するならば $(AB)^{-1} = B^{-1}A^{-1}$.

正則行列たちの積は正則行列になる.
正方行列 $A$ に対し $AB=I$ を満たす $B$ が存在すれば, そのような $B$ は $BA=I$ も満たす (つまり $B=A^{-1}$ となる).
同様に, $BA=I$ なる $B$ は, $B=A^{-1}$ となる.

$A$ を $n$ 次正方行列とする. このとき, 以下が成立する:

$\operatorname{rank}A = n \iff A \text{ は正則}.$
$\operatorname{rank}A \lt n \iff A \text{ は正則でない}.$

$A$ を $n$ 次正方行列とする. このとき, 以下が成立する: \[ A\text{ が正則}\iff A\text{ は基本行列の積で表現される}. \]

ここまでの内容では, ある正方行列 $A$ に逆行列が存在するか否かを判定する方法として,

$AB=I$ (もしくは $BA=I$) を満たす行列 $B$ を見つける (もしくはそのような行列 $B$ が存在しないことを示す),
$A$ の階数を計算する,
$A$ と単位行列 $I$ を並べた拡大行列に対し, 掃き出し法を適用する

を紹介した (ちなみに, 階数の計算は掃き出し法とほぼ同じ計算であり, 逆行列が存在するときにそれを具体的に計算できるかどうかだけ異なる).

ここでは, 逆行列の存在判定 (及び逆行列の具体的な計算) に用いられる 行列式 (determinant) を紹介する. 行列式は正方行列の性質を表現する量であり, 階数と同様に行列に関する重要な指標の一つである. 行列式とは具体的にどのようなものかを説明すると長くなるので, まずは行列式の表記やいくつかの性質から紹介しよう:

正方行列 $A$ の行列式を, \[ \det A \quad (\text{もしくは $|A|$}) \] と表記する. 正方行列でない行列の行列式は定義されない.
$A=(a_{ij})$ の行列式は, \[ \left\lvert\begin{array}{cccc} a_{11} & a_{12} & \dots & a_{1n} \cr a_{21} & a_{22} & \dots & a_{2n} \cr \vdots & \vdots & \ddots& \vdots\cr a_{n1} & a_{n2} &\dots& a_{nn} \end{array}\right\rvert \] などと表記することもある.
実正方行列の行列式は実数である.
$n$ 次正方行列 \[ F(r) =\begin{pmatrix}I_r&O\cr O&O\end{pmatrix} = \begin{pmatrix}1\cr&\ddots\cr&&1\cr&&&0\cr&&&&\ddots\end{pmatrix}
\] に対して, \[ \det F(r) = \left\lbrace\begin{array}{rl} 1&\text{if } r = n,\cr 0&\text{if } r < n \end{array}\right. \] が成立する.
基本行列 $P_{i,j}$, $Q_{i,\lambda}$, $R_{i,j,\lambda}$ に対して, \[ \det P_{i,j} \neq 0,\quad \det Q_{i,\lambda} \neq 0,\quad \det R_{i,j,\lambda} \neq 0
\] が成立する.
二つの $n$ 次正方行列 $A$, $B$ に対して, \[ \det (AB) = (\det A)(\det B) \] が成立する.

これらの性質については, 行列式の定義を述べる際に改めて解説を行う. ひとまず, これらを事実として認めると, 以下が成立することがわかる:

$A$ を $n$ 次正方行列とする. このとき, 以下が成立する: \[ \det A\neq 0\iff \operatorname{rank}A = n \iff A \text{ は正則}. \]

正方行列 $A$ は, 基本行列の積により表される行列 $P$, $Q$ を用いて $A = PF(r)Q$ と表されるのだった (詳細). 上で言及したように, 基本行列の行列式は $0$ でないので, 基本行列の積で表される $P$, $Q$ の行列式も $0$ ではない. これと上に述べた性質より, \[ \begin{array}{rl} \det A\neq 0 &\iff (\det P)(\det F(r))(\det Q)\neq 0 \cr &\iff \det F(r)\neq 0\cr &\iff \operatorname{rank} A=n \end{array} \] が得られる.

すなわち, 正方行列 $A$ の逆行列が存在するか否か判定するには, $A$ の行列式を計算すれば良いことになる. このように, 行列式という概念は逆行列と密接に関連するものであり, 従って連立 $1$ 次方程式とも関連するものである.

ここでは, 行列式の定義を解説し, 定義から得られる性質を紹介する. 行列式の定義は複雑であり, 完璧に理解できなかったとしても仕方ないが, 行列式の計算やその応用は (公式として暗記してでも) できるようになるべきだろう.

3.2: 行列式の定義

行列式が上で述べた性質が満たすように構成するために, (唐突ではあるが) まずは置換という概念を導入する:

$n$ 個の元からなる集合を考える (例えば $\lbrace 1, 2, \dots, n\rbrace$ など). これを並び替える操作を置換 (permutation) という. いま, $\lbrace 1, 2, \dots n\rbrace を \lbrace \sigma(1), \sigma(2), \dots, \sigma(n)\rbrace$ に並び替える置換を \[ \sigma = \begin{bmatrix}1& 2& \dots & n\cr \sigma(1) & \sigma(2) & \dots & \sigma(n)\end{bmatrix} \] と表記する. $n$ 個に対する置換全体を $S_n$ と表記し, $\sigma$ が $n$ 個に対する置換であるとき $\sigma\in S_n$ と表記する.

$\lbrace 1,2,3\rbrace$ に対し, $1$ 番目と $2$ 番目を入れ替えると $\lbrace 2,1,3\rbrace$ という順序になるが, この並び替えは \[ \begin{bmatrix}1&2&3\cr 2&1&3\end{bmatrix}\in S_3 \] と表記される.

$\lbrace 1,2,3\rbrace$ に対し, $1$ 番目と $2$ 番目を入れ替え, その後 $2$ 番目と $3$ 番目を入れ替え, 最後に $3$ 番目と $1$ 番目を入れ替えると $\lbrace 2,3,1\rbrace$ という順序になるが, この並び替えは \[ \begin{bmatrix}1&2&3\cr 2&3&1\end{bmatrix} \in S_3 \] と表記される.

$\lbrace 1,2,3\rbrace$ の置換 $S_3$ は以下の $6$ つからなる: \[ \begin{array}{c}\begin{bmatrix} 1& 2& 3\cr 1 & 2 & 3 \end{bmatrix},\quad \begin{bmatrix} 1& 2& 3\cr 2 & 1 & 3 \end{bmatrix},\cr \begin{bmatrix} 1& 2& 3\cr 1 & 3 & 2 \end{bmatrix},\quad \begin{bmatrix} 1& 2& 3\cr 3 & 2 & 1 \end{bmatrix},\cr \begin{bmatrix} 1& 2& 3\cr 2 & 3 & 1 \end{bmatrix},\quad \begin{bmatrix} 1& 2& 3\cr 3 & 1 & 2 \end{bmatrix}.\end{array} \]

$2$ つの置換 $\sigma$, $\tau$ を合成したもの (つまり $\sigma$ により並び替えたものを $\tau$ によりさらに並び替えたもの) を置換の積といい, $\tau\sigma$ と表記する.

\[ \sigma = \begin{bmatrix}1& 2& 3\cr 2 & 1 & 3\end{bmatrix}, \quad \tau = \begin{bmatrix}1& 2& 3\cr 1 & 3 & 2\end{bmatrix}. \]

$\lbrace 1,2,3\rbrace$ を $\sigma$ により並び替えると $\lbrace 2,1,3\rbrace$ となる.
これをさらに $\tau$ により並び替える, つまり $\lbrace 2,1,3\rbrace$ の $2$ 番目と $3$ 番目を入れ替えると $\lbrace 2,3,1\rbrace$ となる.
つまり $\sigma$ と $\tau$ の合成は $\lbrace 1,2,3\rbrace$ を $\lbrace 2,3,1\rbrace$ に並び替える置換になる.
従って $\tau\sigma = \begin{bmatrix}1&2&3\cr 2&3&1\end{bmatrix}$ となる.

置換の積は右側から先に適用する. 先の例では, $\sigma$ により並び替えたものを $\tau$ で並び替える操作は $\tau\sigma$ と表記される.
一般には $\tau\sigma \neq \sigma\tau$ に注意. 上の例では, $\sigma\tau$ は $\lbrace 1,2,3\rbrace$ を $\lbrace 3,1,2\rbrace$ に並び替える操作であり, \[ \sigma\tau = \begin{bmatrix}1&2&3\cr 3&1&2\end{bmatrix} \neq \tau\sigma. \] である.

$\lbrace 1,2,\dots, n\rbrace$ を並び替えない操作を恒等置換といい, \[ 1_n = \begin{bmatrix}1&2&\dots &n\cr 1&2&\dots & n\end{bmatrix} \] と表記する.
置換 $\sigma$ に対し, $\sigma\tau = \tau\sigma = 1_n$ を満たす置換 $\tau$ を $\sigma$ の逆置換 といい, $\tau=\sigma^{-1}$ と表記する.

置換であって, $2$ つの入れ替えとして表現されるものを互換 (transposition) という.

置換 $\begin{bmatrix}1&2&3\cr 2&1&3\end{bmatrix}$ は, $\lbrace 1,2,3\rbrace$ の $1$ 番目と $2$ 番目を入れ替えたものとみなせるので互換である.

置換 $\begin{bmatrix}1&2&3\cr 2&3&1\end{bmatrix}$ は, $\lbrace 1,2,3\rbrace$ の $2$ つのみ入れ替えたものとして表現できないため互換ではない.

全ての置換は互換の積として表される.

証明略

置換 $\sigma$ が恒等置換であるか, 偶数個の互換の積として表現されるならば, $\sigma$ を偶置換 (even permutation)という.
置換 $\sigma$ が奇数個の互換の積として表現されるならば, $\sigma$ を奇置換 (odd permutation)という.

置換 $\sigma$ に対して, \[ \operatorname{sgn}\sigma = \left\lbrace\begin{array}{rl} 1&\text{if }\sigma \text{ が偶置換},\cr -1&\text{if }\sigma \text{ が奇置換} \end{array}\right. \] を置換 $\sigma$ の符号 (sign, signature) という.

つまり, 置換 $\sigma$ が $n$ 個の互換の積として表現されるならば \[ \operatorname{sgn}\sigma = (-1)^n \] である.

$\operatorname{sgn} \sigma^{-1} = \operatorname{sgn}\sigma$.
$\operatorname{sgn}(\tau\sigma) = (\operatorname{sgn}\sigma)(\operatorname{sgn}\tau)$.

証明略

ここまで準備することで, 正方行列に対する行列式の定義を記述することができる.

$n$ 次正方行列 $A=(a_{ij})$ に対して, \[ \sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) a_{1\sigma(1)} a_{2\sigma(2)}\dots a_{n\sigma(n)} \] を $A$ の行列式といい, $\det A$ (もしくは $|A|$ ) と表記する.

$2$ 次正方行列 $A = \begin{pmatrix}a_{11} & a_{12} \cr a_{21} & a_{22}\end{pmatrix} = \begin{pmatrix}a&b\cr c&d\end{pmatrix}$ を考える. いま, $2$ 個に対する置換 $S_2$ は \[ \sigma_1 = \begin{bmatrix} 1 & 2 \cr \sigma_1(1) & \sigma_1(2) \end{bmatrix} = \begin{bmatrix} 1&2\cr 1&2 \end{bmatrix}, \]\[ \sigma_2 = \begin{bmatrix} 1 & 2 \cr \sigma_2(1) & \sigma_2(2) \end{bmatrix} = \begin{bmatrix} 1&2\cr 2&1 \end{bmatrix} \] からなる. ここで, \[ \operatorname{sgn}\sigma_1 = 1,\quad \operatorname{sgn} \sigma_2 = -1 \] であることから, \[ \begin{array}{rl}\det A &= (\operatorname{sgn}\sigma_1) a_{1\sigma_1(1)} a_{2\sigma_1(2)} \cr &\qquad + (\operatorname{sgn}\sigma_2) a_{1\sigma_2(1)} a_{2\sigma_2(2)} \cr &= a_{11}a_{22} - a_{12}a_{21}\cr &= ad-bc \end{array} \] となる.

$3$ 次正方行列 $A = (a_{ij}) = \begin{pmatrix}a&b&c\cr d&e&f\cr g&h&i\end{pmatrix}$ を考える. いま $S_3$ は先の例に挙げた \[ \begin{array}{c}\sigma_1 = \begin{bmatrix} 1& 2& 3\cr 1 & 2 & 3 \end{bmatrix},\quad \sigma_2 = \begin{bmatrix} 1& 2& 3\cr 2 & 1 & 3 \end{bmatrix},\cr \sigma_3 = \begin{bmatrix} 1& 2& 3\cr 1 & 3 & 2 \end{bmatrix},\quad \sigma_4 = \begin{bmatrix} 1& 2& 3\cr 3 & 2 & 1 \end{bmatrix},\cr \sigma_5 = \begin{bmatrix} 1& 2& 3\cr 2 & 3 & 1 \end{bmatrix},\quad \sigma_6 = \begin{bmatrix} 1& 2& 3\cr 3 & 1 & 2 \end{bmatrix}.\end{array} \] の$6$ つであり, これらを用いて計算すると \[ \begin{array}{rl}\det A &= (\operatorname{sgn}\sigma_1) a_{1\sigma_1(1)}a_{2\sigma_1(2)}a_{3\sigma_1(3)} \cr &\quad + (\operatorname{sgn}\sigma_2) a_{1\sigma_2(1)}a_{2\sigma_2(2)}a_{3\sigma_2(3)} \cr &\qquad + (\operatorname{sgn}\sigma_3) a_{1\sigma_3(1)}a_{2\sigma_3(2)}a_{3\sigma_3(3)} \cr &\quad + (\operatorname{sgn}\sigma_4) a_{1\sigma_4(1)}a_{2\sigma_4(2)}a_{3\sigma_4(3)} \cr &\qquad + (\operatorname{sgn}\sigma_5) a_{1\sigma_5(1)}a_{2\sigma_5(2)}a_{3\sigma_5(3)} \cr &\quad\qquad + (\operatorname{sgn}\sigma_6) a_{1\sigma_6(1)}a_{2\sigma_6(2)}a_{3\sigma_6(3)}\cr &= a_{11} a_{22} a_{33} - a_{12} a_{21} a_{33} \cr &\quad - a_{11} a_{23} a_{32} - a_{13} a_{22} a_{31} \cr & \qquad + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} \cr &= aei + bfg + cdh \cr & \qquad - ceg - bdi - afh \end{array} \] となる.

$4$ 次以上の正方行列に対しても, 上と同様に定義から行列式を計算することは可能だが, 実用上は (いくつかの特殊な場合を除いて) $2$ 次と $3$ 次の場合の行列式の定義を公式として暗記すれば十分だろう: \[ A = \begin{pmatrix}a&b\cr c&d\end{pmatrix} \leadsto \det A = ad-bc. \]\[ A = \begin{pmatrix}a&b&c\cr d&e&f\cr g&h&i\end{pmatrix} \leadsto \begin{array}{rl}\det A\hspace{-12px}&= aei + bfg + cdh \cr &\quad - ceg - bdi - afh.\end{array} \] ちなみに $1$ 次正方行列は, その唯一の成分である複素数と同一視されるが, 行列式もこれに一致する: \[ A =\begin{pmatrix}a\end{pmatrix}\leadsto \det A = a \]

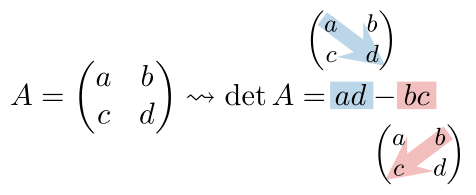
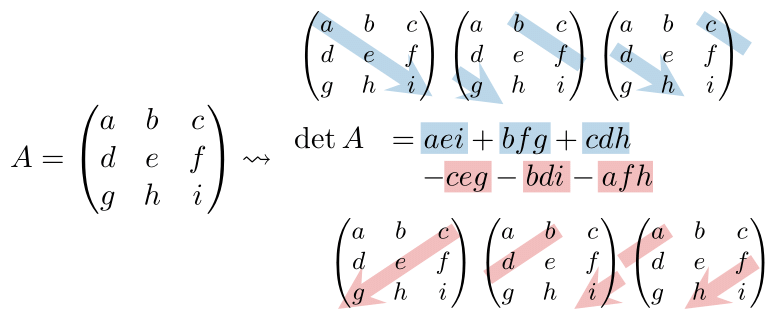
3.3: 行列式の性質

行列式の性質を列挙していく. 行列式を定義に置換という概念を用いたのは, 以下の性質たちが成立するように構成するためである.

対角行列の行列式は, その対角成分の積に等しい.

$A = (a_{ij})$ を対角行列とすると, 対角行列の定義より \[ a_{ij} = 0 \quad \text{ if }\quad i\neq j \] である. 従って, 行列式の定義 \[ \det A = \sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) a_{1\sigma(1)} a_{2\sigma(2)}\dots a_{n\sigma(n)} \] において, $\sigma(1)=1$, $\sigma(2)=2$, $\dots$, $\sigma(n)=n$ の場合を除き $a_{1\sigma(1)} a_{2\sigma(2)}\dots a_{n\sigma(n)}=0$ となる. 従って, 対角行列 $A$ に対して \[ \det A = a_{11} a_{22} \dots a_{nn} \] となる.

\[ A = \begin{pmatrix} a&0&0\cr 0&b&0\cr 0&0&c\end{pmatrix}. \] このとき, \[ \begin{array}{rl}\det A &= abc + 0\cdot0\cdot0 + 0\cdot0\cdot0 \cr &\qquad - 0\cdot b\cdot0 - 0\cdot0\cdot c - a\cdot 0\cdot0 \cr &= abc\end{array} \]

特に, $\det O = 0$ および $\det I = 1$ が成立する.

基本行列 $Q_{i,\lambda}$ について, $\det Q_{i,\lambda} = \lambda\neq0$ を確かめることができる. また, \[ F(r) =\begin{pmatrix} I_r&O\cr O&O \end{pmatrix}\in\mathbb{R}^{n\times n} \] について, \[ \det F(r) = \left\lbrace\begin{array}{rl} 1&\text{if } r = n,\cr 0&\text{if } r < n \end{array}\right. \] も確かめられる.

$n$ 次正方行列 $A$ と複素数 $\lambda$ に対し, \[ \det(\lambda A) = \lambda^n \det A \] が成立する.

行列 $\lambda A$ の $(i,j)$ 成分は, $A$ の $(i,j)$ 成分の $\lambda$ 倍なので, \[ \begin{array}{rl}\det (\lambda A) &= \displaystyle\sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) (\lambda a_{1\sigma(1)}) (\lambda a_{2\sigma(2)})\dots (\lambda a_{n\sigma(n)})\cr &= \lambda^n \displaystyle\sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) a_{1\sigma(1)} a_{2\sigma(2)}\dots a_{n\sigma(n)} \cr &= \lambda^n\det A \end{array} \] となる.

単位行列 $I\in\mathbb{R}^{n\times n}$ に対して $\det (-I) = (-1)^n$.
$\det\begin{pmatrix} \lambda a&\lambda b\cr \lambda c&\lambda d \end{pmatrix} = (\lambda a)(\lambda d) - (\lambda b)(\lambda c)$
$\begin{array}{rl} \hspace{91px} &= \lambda^2(ad-bc)\cr &= \lambda^2\det\begin{pmatrix} a&b\cr c&d \end{pmatrix}. \end{array}$

正方行列 $A$ に対し, \[ \det A^{\operatorname{T}} = \det A \] が成立する.

全ての $\sigma\in S_n$ に対し, 対応する $\sigma^{-1}\in S_n$ が存在する. これと $\operatorname{sgn}\sigma = \operatorname{sgn}\sigma^{-1}$ を用いると, \[ \begin{array}{rl}\det A &= \displaystyle\sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) a_{1\sigma(1)} a_{2\sigma(2)}\dots a_{n\sigma(n)} \cr &= \displaystyle\sum_{\sigma\in S_n}(\operatorname{sgn}\sigma^{-1}) a_{1\sigma^{-1}(1)} a_{2\sigma^{-1}(2)} \dots a_{n\sigma^{-1}(n)} \cr &= \displaystyle\sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) a_{\sigma(1)1} a_{\sigma(2)2} \dots a_{\sigma(n)n} \end{array} \] となる, ここで, 最後の等号では $\sigma^{-1}(i) = j$ であるときに $a_{i\sigma^{-1}(i)} = a_{\sigma(j)j}$ であることを用い, また $a_{\sigma(j)j}$ たちの積の順序を入れ換えている.

一方で, 転置 $A^{\operatorname{T}}$ の $(i,j)$ 成分を $\widetilde{a}_{ij}$ とおくと, $\widetilde{a}_{ij} = a_{ji}$ となるため, \[ \begin{array}{rl}\det A^{\operatorname{T}} &= \displaystyle\sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) \widetilde{a}_{1\sigma(1)} \widetilde{a}_{2\sigma(2)}\dots \widetilde{a}_{n\sigma(n)} \cr &= \displaystyle\sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) a_{\sigma(1)1} a_{\sigma(2)2} \dots a_{\sigma(n)n} \end{array} \] である. 従って, $\det A = \det A^{\operatorname{T}}$ が得られる.

$\det\begin{pmatrix} a & b \cr c & d \end{pmatrix}^{\operatorname{T}} = \det\begin{pmatrix} a & c \cr b & d \end{pmatrix}$
$\begin{array}{rl} \hspace{82px} & = ad-bc\cr &= \det\begin{pmatrix} a & b \cr c & d \end{pmatrix} \end{array}$

上の結果より, $A$ の行列式を考える際に $A$ の列に関する性質は, (転置を考えることで) $A$ の行に対しても同様に成立することが言える. そこで, 行列 $A$ を第 $j$ 列ベクトル $\mathbf{a}_j$ を横に並べたものとみなす:

\[ \det A = \det (\mathbf{a}_1, \mathbf{a}_2, \dots, \mathbf{a}_n). \]

この表記を用いると, 行列式の多重線形性を以下のように説明することができる:

行列の第 $j$ 列ベクトルが $2$ つの列ベクトルの和で表されるとき,
行列の第 $j$ 列ベクトルがベクトルのスカラー倍で表されるとき,

証明略 (行列式の定義より得られる, 行に対しても同様の性質が成り立つことに注意)

行に対しても同様に多重線形性が成り立つ:
$\det\begin{pmatrix} a&b\cr 0&0 \end{pmatrix} = 0\det\begin{pmatrix} a&b\cr \ast&\ast \end{pmatrix} = 0.$

基本行列 $R_{i,j,\lambda}$ に対して, \[ \begin{array}{rl} \det R_{i,j,\lambda} &= \det I + \det (\mathbf{0},\dots,\mathbf{0}, \lambda\mathbf{e}_i,\mathbf{0}, \dots\mathbf{0}) \cr & = 1 (\neq 0) \end{array} \] を確かめることができる.

置換 $\tau\in S_n$ に対し, \[ \det (\mathbf{a}_{\tau(1)}, \dots, \mathbf{a}_{\tau(n)}) = (\operatorname{sgn}\tau) \det (\mathbf{a}_1, \dots, \mathbf{a}_n). \] が成立する.

全ての置換は互換の積として表されるため, $i$ 番目と $j$ 番目を入れ替える互換 $\tau$ に対し \[ \det (\mathbf{a}_1, \dots, \mathbf{a}_i, \dots, \mathbf{a}_j, \dots, \mathbf{a}_n) = - \det (\mathbf{a}_1, \dots, \mathbf{a}_j, \dots, \mathbf{a}_i, \dots, \mathbf{a}_n) \] となることを示せば良い. 互換 $\sigma\in S_n$ に対し, $\widetilde{\sigma} = \tau\sigma$ とおくと, \[ \begin{array}{rl} &\det (\mathbf{a}_1, \dots, \mathbf{a}_j, \dots, \mathbf{a}_i, \dots, \mathbf{a}_n) \cr &\quad= \displaystyle\sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) a_{1\tau\sigma(1)} \dots a_{n\tau\sigma(n)} \cr &\quad= (\operatorname{sgn}\tau)\displaystyle\sum_{\widetilde{\sigma}\in S_n}(\operatorname{sgn}\widetilde{\sigma}) a_{1\widetilde{\sigma}(1)} \dots a_{n\widetilde{\sigma}(n)} \cr &\quad = - \det (\mathbf{a}_1, \dots, \mathbf{a}_i, \dots, \mathbf{a}_j, \dots, \mathbf{a}_n), \end{array} \] ここで全ての $\sigma\in S_n$ についての足し合わせは, 全ての $\widetilde{\sigma}\in S_n$ についての足し合わせに等しいことを用いた.

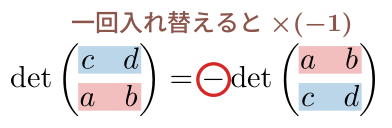
上の証明中にも言及しているが, ある正方行列 $A$ の第 $i$ 列と第 $j$ 列 (もしくは第 $i$ 行と第 $j$ 行) を入れ換えた行列を $\widetilde{A}$ とすると, \[ \det \widetilde{A} = -\det A \] が成立する.
また, 上の結果は, 列 (もしくは行) に対する入れ換えを $k$ 回行った行列 $\widehat{A}$ に対して \[ \det\widehat{A} = (-1)^k \det A \] となることを意味している.
基本行列 $P_{i,j}$ に対して, \[ \det P_{i,j} = -\det I = -1 (\neq 0) \] を確かめることができる

\[ \begin{array}{rl} \det\begin{pmatrix} c&d \cr a&b \end{pmatrix} &= bc - ad \cr &= -(ad-bc) \cr &= -\det\begin{pmatrix} a&b \cr c&d \end{pmatrix}. \end{array} \]

正方行列 $A$ の異なる $2$ つの列 (もしくは行) が一致するならば $\det A=0$.

行列 $A$ の第 $i$ 列ベクトルと第 $j$ 列ベクトルが等しいならば, それらを入れ換えた行列が $A$ に一致する. これと交代性より $\det A = -\det A$ となるため, $\det A=0$ である.

正方行列 $A$ の第 $i$ 列に第 $j$ 列の (もしくは第 $i$ 行に第 $j$ 行の) $\lambda$ 倍を加えて得られる行列 $\widetilde{A}$ に対し, \[ \det\widetilde{A} = \det A \] が成立する.

列の場合のみ証明する. 行列 $A = (\mathbf{a}_1, \dots, \mathbf{a}_n)$ に対し, \[ \widetilde{A} = (\mathbf{a}_1, \dots, \mathbf{a}_i + \lambda\mathbf{a}_j, \dots, \mathbf{a}_n) \] と表すことができるので, \[ \begin{array}{rl} \det \widetilde{A} &= \det (\mathbf{a}_1, \dots, \mathbf{a}_i, \dots, \mathbf{a}_n) \cr & \qquad + \det (\mathbf{a}_1, \dots, \lambda\mathbf{a}_j, \dots, \mathbf{a}_n) \cr &= \det A \cr & \qquad + \lambda \det (\mathbf{a}_1, \dots, \mathbf{a}_j, \dots, \mathbf{a}_j, \dots, \mathbf{a}_n). \end{array} \] ここで, 第 $2$ 項の行列式は先の結果より $0$ となるため, 欲しい結果が得られる.

\[ A = \begin{pmatrix} 1&2\cr 2&4 \end{pmatrix} \]

この行列の第 $2$ 行に第 $1$ 行の $-2$ 倍を加えて得られる行列 $\widetilde{A}$ は \[ \widetilde{A} = \begin{pmatrix} 1&2 \cr 0&0 \end{pmatrix} \] である.
ここで, 定理より $\det A = \det\widetilde{A}$ が成立する. 実際に計算すると, どちらも $0$ となることを確かめられる.

この結果は, 基本行列 $R_{i,j,\lambda}$ に対して \[ \det(R_{i,j,\lambda} A) = \det A,\quad \det(AR_{i,j,\lambda}) = \det A \] であることを意味している.

\[ A = \begin{pmatrix} 1 & 11 & 111 \cr 0 & 1 & 11 \cr 0 & 0 & 1 \end{pmatrix}. \] このとき, \[ \begin{array}{rll} \det A &= \det \begin{pmatrix}1 & 11 & 111 \cr 0 & 1 & 11 \cr 0 & 0 & 1\end{pmatrix} & \cr &= \det \begin{pmatrix}1 & 0 & 111 \cr 0 & 1 & 11 \cr 0 & 0 & 1\end{pmatrix} & \left(\begin{array}{c}\text{第 $2$ 列に第 $1$ 列の}\cr \text{$-11$ 倍を加えた}\end{array}\right) \cr &= \det \begin{pmatrix}1 & 0 & 0 \cr 0 & 1 & 11 \cr 0 & 0 & 1\end{pmatrix} & \left(\begin{array}{c}\text{第 $3$ 列に第 $1$ 列の}\cr \text{$-111$ 倍を加えた}\end{array}\right) \cr &= \det \begin{pmatrix}1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1\end{pmatrix} & \left(\begin{array}{c}\text{第 $3$ 列に第 $2$ 列の}\cr \text{$-11$ 倍を加えた}\end{array}\right) \cr &= \det I = 1. \end{array} \]

3.1: 逆行列の存在 においてあらかじめ言及した行列式の性質のうち, 次が最後のものである:

同じ型の $2$ つの正方行列 $A$, $B$ に対して \[ \det (AB) = \det A\det B \] が成立する.

行列 $B$ の第 $j$ 列ベクトルを $\mathbf{b}_j$ とする. また, 標準基底 $\mathbf{e}_i$ を用いて $\mathbf{b}_j = \displaystyle\sum_{ {i_j} =1}^n b_{ {i_j} j} \mathbf{e}_{i_j}$ とおく. このとき, \[ \det (AB) = \det (A\mathbf{b}_1, \dots, A\mathbf{b}_n). \] 多重線形性より \[ \begin{array}{rl} \det (A\mathbf{b}_1, \dots, A\mathbf{b}_n) &= \displaystyle\sum_{i_1}^n b_{ {i_1} 1}\det (A\mathbf{e}_{i_1}, A\mathbf{b}_2, \dots, A\mathbf{b}_n) \cr & =\dots\cr &= \displaystyle\sum_{i_1}^n\dots\sum_{i_n}^n b_{ {i_1 } 1}\dots b_{ {i_n} n} \det (A\mathbf{e}_{i_1}, \dots, A\mathbf{e}_{i_n}). \end{array} \] ここで, もしも $i_1,\dots, i_n$ の中に同じものが複数あったならば, $2$ つの列が一致することになるため $\det (A\mathbf{e}_{i_1}, \dots, A\mathbf{e}_{i_n}) = 0$ となる. 一方, $i_1, \dots, i_n$ が全て異なる場合, そのような並び方と同一視できる置換 $\sigma\in S_n$ が存在する. まとめると, 上の式の足し合わせの中で $0$ でないものは $\sigma\in S_n$ を用いて表すことができるもののみであり, 具体的には \[ \det (A\mathbf{b}_1, \dots, A\mathbf{b}_n) = \displaystyle\sum_{\sigma\in S_n} b_{\sigma(1)1} \dots b_{\sigma(n)n} \det (A\mathbf{e}_{\sigma(1)}, \dots, A\mathbf{e}_{\sigma(n)}) \] となる. ここで, 交代性より \[ \begin{array}{rl} \det (A\mathbf{e}_{\sigma(1)}, \dots, A\mathbf{e}_{\sigma(n)}) &= (\operatorname{sgn}\sigma) \det(A\mathbf{e}_1, \dots, A\mathbf{e}_n)\cr &= (\operatorname{sgn}\sigma) \det A \end{array} \] となり, 以上より \[ \begin{array}{rl} \det (AB) &= \det A \displaystyle\sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) b_{\sigma(1)1} \dots b_{\sigma(n)n} \cr & = \det A\det B^{\operatorname{T}}\cr &= \det A\det B \end{array} \] が得られる (転置により行列式は変わらないことを用いた).

ここまでに示した性質を組み合わせることで, 以下が得られるのだった (既に証明済み):

$A$ を $n$ 次正方行列とする. このとき, 以下が成立する: \[ \det A\neq 0\iff A \text{ は正則}. \]

\[ A = \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix},\qquad B = \begin{pmatrix} 1&2\cr 2&4 \end{pmatrix}. \]

$\det A = 1\cdot 4 - 2\cdot 3 = -2\neq0$, 従って逆行列が存在する.
- 実際, $A^{-1} = \begin{pmatrix}-2&1\cr 3/2&-1/2\end{pmatrix}$ であることが確かめられる.
一方, $\det B = 1\cdot 4 - 2\cdot 2 = 0$ であり, 従って逆行列を持たない.

3.4: 余因子行列とクラメルの公式

行列式を用いると, ある正方行列が正則であるか否かを比較的容易に判定することができる. ただし, 定義に基づく行列式の計算は, 行列のサイズが大きくなるほど困難となる.

ここでは, 行列式の計算する際のテクニックを紹介し, また行列式の応用の一つとして, 行列式を用いて逆行列を計算する方法も紹介する.

$n$ 次正方行列 $A$ と $n-1$ 次正方行列 $B$ に対して, もしもブロック行列を用いて

\[ A = \begin{pmatrix} a_{11} & \mathbf{0} \cr * & B \end{pmatrix} \]

と表されるならば,

\[ \det A = a_{11}\det B \]

が成立する, ここで $\mathbf{0}\in\mathbb{R}^{1\times (n-1)}$ は行ベクトルであり, $*\in\mathbb{R}^{(n-1)\times 1}$ は任意の列ベクトルである.

転置により行列式は変わらないため,

\[ A = \begin{pmatrix} a_{11} & * \cr \mathbf{0} & B \end{pmatrix} \]

のときも同様に

\[ \det A = a_{11}\det B \]

が成立する. ただし, このときは $\mathbf{0}\in\mathbb{R}^{(n-1)\times 1}$ は列ベクトルであり, $*\in\mathbb{R}^{1\times(n-1)}$ は任意の行ベクトルである.

行列 $A$ が

\[ A = \begin{pmatrix} a_{11} & \mathbf{0} \cr * & B \end{pmatrix} \]

と表されるとき,

\[ \det A = \sum_{\sigma\in S_n}(\operatorname{sgn}\sigma) a_{1\sigma(1)} a_{2\sigma(2)} \dots a_{n\sigma(n)} \]

の足し合わせの項は, $\sigma(1) = 1$ である場合を除き $0$ となる. いま, $\sigma\in S_n$ であって $\sigma(1)=1$ であるものは, $\widetilde{\sigma}\in S_{n-1}$ と同一視することができる (ただし, $\widetilde{\sigma}$ は $\lbrace2,\dots,n\rbrace$ の置換とみなすことにする). この同一視に基づくと,

\[ \det A = a_{11}\sum_{\widetilde{\sigma}\in S_{n-1}}(\operatorname{sgn}\widetilde{\sigma}) a_{2\widetilde{\sigma}(2)} \dots a_{n\widetilde{\sigma}(n)} \] となり, ここで \[ \displaystyle\sum_{\widetilde{\sigma}\in S_{n-1}}(\operatorname{sgn}\widetilde{\sigma}) a_{2\widetilde{\sigma}(2)} \dots a_{n\widetilde{\sigma}(n)} \] という足し合わせは, 行列式の定義より \[ \det\begin{pmatrix} a_{22} & \dots & a_{2n} \cr \vdots & \ddots & \vdots \cr a_{n2} & \dots & a_{nn} \end{pmatrix}, \] つまりこの場合は $\det B$ と一致する.

以降, この性質を便宜上 "行列式の計算における行列サイズ削減" と呼ぶことにする. ただし, この呼び方はここだけのものであり, 他では通用しないため注意.

\[ A = \begin{pmatrix} 0 & 3 & 0 & 0 \cr 2 & 4 & 1 & 4 \cr 0 & 2 & 1 & 2 \cr 2 & 6 & 1 & 6\end{pmatrix}. \] この行列の行列式は, 例えば以下のように計算できる: \[ \begin{array}{rll} \det A &= \det \begin{pmatrix} 0 & 3 & 0 & 0 \cr 2 & 4 & 1 & 4 \cr 0 & 2 & 1 & 2 \cr 2 & 6 & 1 & 6 \end{pmatrix} & \cr &= -\det \begin{pmatrix} 3 & 0 & 0 & 0 \cr 4 & 2 & 1 & 4 \cr 2 & 0 & 1 & 2 \cr 6 & 2 & 1 & 6 \end{pmatrix} & \text{(第 $1$ 列と第 $2$ 列を交換)} \cr &= -3 \det\begin{pmatrix} 2 & 1 & 4 \cr 0 & 1 & 2\cr 2 & 1 & 6 \end{pmatrix} &\text{(行列サイズ削減)}\cr &= -3 \det\begin{pmatrix} 2 & 1 & 4 \cr 0 & 1 & 2 \cr 0 & 0 & 2 \end{pmatrix} &\left(\begin{array}{c}\text{第 $3$ 行に第 $1$ 行の}\cr \text{$-1$ 倍を加えた}\end{array}\right) \cr &= -6 \det\begin{pmatrix} 1&2\cr 0&2 \end{pmatrix} &\text{(行列サイズ削減)} \cr &= -12 \end{array} \] と計算できる.

この性質は, 成分が全て数値である行列の行列式を計算する際に非常に便利である. 一方で, 成分が文字で表されている場合には有用で無い場合がある.

\[ A = \begin{pmatrix} 0 & a & b & c \cr -a & 0 & d & e \cr -b & -d & 0 & f \cr -c & -e & -f & 0 \end{pmatrix}. \]

この行列の行列式を, 行列サイズ削減を用いて計算しようとしてみる.
例えば, 第 $1$ 列と第 $2$ 列を交換して
もしも $a\neq0$ ならば, 第 $3$ 行に第 $1$ 行の $d/a$ 倍を加え, 第 $4$ 行に第 $1$ 行の $e/a$ 倍を加えることで

行列サイズを削減することはできるが, 行列の成分は複雑なものになってしまう.
また, この変形は $a\neq0$ のときのみ可能であり, $a=0$ のときは場合分けが必要となる.

このように, 成分が文字で表現されている行列に対しては, 行列サイズ削減を用いた行列式の計算は必ずしも容易ではない.

そこで, 上のような場合にも行列式を容易に計算することができるように, 行列サイズ削減の一般化を考えよう.

$n$ 次正方行列 $A$ に対し, その第 $i$ 行と第 $j$ 列を取り除くことで得られる $n-1$ 次正方行列の行列式を第 $(i,j)$ 小行列式 (minor determinant) という. また, $(i,j)$ 小行列式に $(-1)^{i+j}$ をかけたものを第 $(i,j)$ 余因子 (cofactor) という.

\[ A = \begin{pmatrix} 1&2&3\cr 4&5&6\cr 7&8&9 \end{pmatrix}. \]

この行列の第 $(1,1)$ 小行列式は \[ \begin{pmatrix} \square & \square& \square \cr \square & 5 & 6\cr \square & 8& 9 \end{pmatrix}, \quad \text{つまり} \quad \begin{pmatrix} 5&6\cr 8&9 \end{pmatrix} \] の行列式であり, 従って第 $(1,1)$ 余因子は \[ (-1)^{1+1} \det\begin{pmatrix} 5&6\cr 8&9 \end{pmatrix} = -3. \]
この行列の第 $(2,2)$ 小行列式は \[ \begin{pmatrix} 1 & \square& 3 \cr \square & \square & \square\cr 7 & \square& 9 \end{pmatrix}, \quad \text{つまり} \quad \begin{pmatrix} 1&3\cr 7&9 \end{pmatrix} \] の行列式であり, 従って第 $(2,2)$ 余因子は \[ (-1)^{2+2} \det\begin{pmatrix} 1&3\cr 7&9 \end{pmatrix} = -12. \]

\[ A = \begin{pmatrix} a_{11} & \mathbf{0} \cr * & B \end{pmatrix} \]

この行列の第 $(1,1)$ 小行列式は, 行列 $A$ の第 $1$ 行と第 $1$ 列を取り除いた正方行列 $B$ の行列式であり, 従って第 $(1,1)$ 小行列式は

\[ (-1)^{1+1}\det B = \det B. \]

$n$ 次正方行列 $A=(a_{ij})$ の $(i,j)$ 余因子を $\widetilde{a}_{ij}$ とおく, このとき

任意の $j$ に対し, (第 $j$ 列に注目すると) \[ \begin{array}{rl} \det A &= a_{1j} \widetilde{a}_{1j} + \dots + a_{nj} \widetilde{a}_{nj} \cr &= \displaystyle\sum_{i=1}^n a_{ij} \widetilde{a}_{ij} \end{array} \] が成立する.
任意の $i$ に対し, (第 $i$ 行に注目すると) \[ \begin{array}{rl} \det A &= a_{i1} \widetilde{a}_{i1} + \dots + a_{in} \widetilde{a}_{in} \cr &= \displaystyle\sum_{j=1}^n a_{ij} \widetilde{a}_{ij} \end{array} \] が成立する.

上のみ証明する. 以降, 行列 $A$ の第 $(i,j)$ 小行列式を $d_{ij}$ と表記し, 第 $(i,j)$ 余因子を $\widetilde{a}_{ij}$ と表記することにする.

$j=1$ のとき: 多重線形性より, \[ \begin{array}{rl} \det A &= \det\begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \cr 0 & a_{22} & \dots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr 0 & a_{n2} & \dots & a_{nn} \end{pmatrix} \cr &\qquad + \det\begin{pmatrix} 0 & a_{12} & \dots & a_{1n} \cr a_{21} & a_{22} & \dots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr 0 & a_{n2} & \dots & a_{nn} \end{pmatrix} \cr & \qquad \qquad + \dots + \det\begin{pmatrix} 0 & a_{12} & \dots & a_{1n} \cr 0 & a_{22} & \dots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr a_{n1} & a_{n2} & \dots & a_{nn} \end{pmatrix} \end{array} \] となる. 第 $1$ 項は行列サイズ削減より $a_{11} d_{11}$, すなわち $a_{11}\widetilde{a}_{11}$ に等しい. 第 $2$ 項は交代性も用いて \[ \begin{array}{rl} \det\begin{pmatrix} 0 & a_{12} & \dots & a_{1n} \cr a_{21} & a_{22} & \dots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr 0 & a_{n2} & \dots & a_{nn} \end{pmatrix} &= - \det\begin{pmatrix} a_{21} & a_{22} & \dots & a_{2n} \cr 0 & a_{12} & \dots & a_{1n} \cr \vdots & \vdots & \ddots & \vdots \cr 0 & a_{n2} & \dots & a_{nn} \end{pmatrix} \cr &= -a_{21} d_{21} \cr & = (-1)^3 a_{21} d_{21} \cr &= a_{21}\widetilde{a}_{21}. \end{array} \] 同様に, 第 $i$ 項は $(-1)^{i+1}a_{i1} d_{i1}$, すなわち $a_{i1}\widetilde{a}_{i1}$ に等しいので欲しい式が得られる.
$j\neq1$ のとき: 第 $j$ 列と第 $j-1$ 列を入れ換え, その後に第 $j-1$ 列を第 $j-2$ 列と入れ換え, ... , 最後に第 $2$ 列と第 $1$ 列を入れ換えるという操作により, 第 $j$ 列を第 $1$ 列に移動することがでる. この操作は列の入れ替えを $j-1$ 回行うため, この行列の行列式は $(-1)^{j-1}\det A$ となる. あとは上と同様に計算すると, \[ (-1)^{j-1}\det A = a_{1j}d_{1j} - a_{2j}d_{2j} + \dots + (-1)^n a_{nj}d_{nj}. \] 両辺を $(-1)^{j+1}$ 倍することで, \[ \begin{array}{rl} \det A &= (-1)^{2j}\det A \cr &= (-1)^{j+1} a_{1j} d_{1j} + (-1)^{j+2} a_{2j} d_{2j} + \dots + (-1)^{j+n} a_{nj} d_{nj} \cr &= a_{1j} \widetilde{a}_{1j} + \dots + a_{nj} \widetilde{a}_{nj} \end{array} \] となり欲しい式が得られる.

\[ A = (a_{ij}) = \begin{pmatrix} a&b&c \cr d&e&f \cr g&h&i \end{pmatrix}. \]

このとき, \[ \begin{array}{rl} \det A &= aei+bfg+cdh \cr & \quad -ceg-bdi-afh \end{array} \] であった.
これを余因子展開により確かめてみる: 例えば第 $1$ 列に注目すると \[ \det A = \displaystyle\sum_{i=1}^3 a_{i1}\widetilde{a}_{i1} \] である. これを用いて計算してみると, \[ \begin{array}{rl} \det A &= a (-1)^{1+1}\det\begin{pmatrix} \square & \square & \square \cr \square & e & f \cr \square & h & i \end{pmatrix} \cr & \quad + d (-1)^{2+1}\det\begin{pmatrix} \square & b & c \cr \square & \square & \square \cr \square & h & i \end{pmatrix} \cr & \qquad + g(-1)^{3+1}\det\begin{pmatrix} \square & b & c \cr \square & e & f \cr \square & \square & \square \end{pmatrix} \cr &= a\det\begin{pmatrix} e&f \cr h&i \end{pmatrix} - d\det\begin{pmatrix} b&c \cr h&i \end{pmatrix} + g\det\begin{pmatrix} b&c \cr e&f \end{pmatrix} \cr &= a(ei-fh) - d(bi-ch) + g(bf-ce) \cr &= aei + bfg + cdh - ceg - bdi - afh \end{array} \] となり, 確かに同じ結果が得られる.

\[ A = \begin{pmatrix} a_{11} & \mathbf{0} \cr * & B \end{pmatrix} \]

$a_{12} = \dots = a_{1n} = 0$ に注目すると, 第 $1$ 行に注目した余因子展開より

\[ \begin{array}{rl} \det A &= a_{11}\widetilde{a}_{11} + 0\cdot\widetilde{a}_{12} + \dots + 0\cdot\widetilde{a}_{1n} \cr &= a_{11}\widetilde{a}_{11}. \end{array} \]

ここで, $\widetilde{a}_{11} = \det B$ なので, この場合は

\[ \det A = a_{11}\det B \]

が得られる. つまり, 行列サイズ削減は余因子展開の特別な場合であると解釈できる.

余因子展開による行列式の計算は, 各余因子が簡単に計算できる場合や, 行列の成分が文字で表されている場合に有用である. 一方で, この定理よりもむしろ行列サイズ削減の方が使い勝手が良い場面も多いだろう.

次に, 余因子を応用して逆行列を計算する方法を紹介する. まず, 余因子行列 の定義を述べる:

$n$ 次正方行列 $A$ に対し, 第 $(i,j)$ 成分が $A$ の第 $(j,i)$ 余因子 $\widetilde{a}_{ji}$ である $n$ 次正方行列を $A$ の余因子行列 (adjugate matrix) といい, $\operatorname{adj} A$ と表記する.

$A$ の余因子行列 $\operatorname{adj} A$ は $\widetilde{A}$ と表記されることも多いが, ここでは第 $(i,j)$ 成分が $A$ の第 $(i,j)$ 余因子 $\widetilde{a}_{ij}$ である行列を $\widetilde{A}$ と表すことにする. このとき, $\operatorname{adj} A = \widetilde{A}^{\operatorname{T}}$ である.

余因子行列の性質をいくつか紹介しておく.

$\operatorname{adj}O = O$.
$\operatorname{adj}I = I$.
$\operatorname{adj}(\lambda A) = \lambda^{n-1}\operatorname{adj}A$, ここで　$A$ は $n$ 次正方行列.
$\operatorname{adj}(A^{\operatorname{T}}) = (\operatorname{adj}A)^{\operatorname{T}}$.

証明略

特に, 以下の性質が重要となる.

$n$ 次正方行列 $A$ に対し, \[ A(\operatorname{adj}A) =(\operatorname{adj}A)A = (\det A)I. \] が成立する.

行列 $A(\operatorname{adj}A)$ の第 $(i,j)$ 成分は \[ \displaystyle\sum_{k=1}^n a_{ik} \widetilde{a}_{jk} \] となり, $i=j$ ならば余因子展開より $\det A$ と一致する. もしも $i\neq j$ ならば, これは $A$ の第 $j$ 行を第 $i$ 行で置き換えた行列の余因子展開と一致するが, そのような行列は第 $i$ 行と第 $j$ 行が等しいため行列式が $0$ になる. 従って $A(\operatorname{adj}A) = (\det A)I$ が得られる. $(\operatorname{adj}A)A = (\det A)I$ も同様にして証明される.

この結果を $\det A$ の計算に応用することができる場合もあるが, これが有用な場面は限られる.

この結果と $\det A\neq0\iff A$ が正則である, という性質を用いると以下が得られる:

正則行列 $A$ に対し, \[ A^{-1} = \dfrac{1}{\det A}\operatorname{adj} A \] が成立する.

\[ A = \begin{pmatrix}a & b \cr c & d\end{pmatrix}. \]

行列 $A$ が正則行列であるとする, つまり $\det A = ad-bc\neq 0 $ とする.
このとき, \[ A^{-1} = \dfrac{1}{ad-bc}\begin{pmatrix} d & -b \cr -c & a \end{pmatrix} \]
実際に, $AA^{-1} = I$ や $A^{-1}A = I$ となることを確かめることができる.

この結果を応用することで, 連立 $1$ 次方程式の解法の一つが得られる:

正則行列 $A$ に対し, 連立 $1$ 次方程式 \[ A\mathbf{x} = \mathbf{b} \] の (ただ一つの) 解 $\mathbf{x}$ の各成分 $x_i$ は次で与えられる: \[ x_i = \dfrac{\det A_i}{\det A}, \] ここで, $A_i$ は行列 $A$ の第 $i$ 列を $\mathbf{b}$ に置き換えた行列である.

上の結果より, \[ \mathbf{x} = A^{-1}\mathbf{b} = \dfrac{1}{\det A}(\operatorname{adj}A)\mathbf{b} \] である. ここで, 余因子行列 $\operatorname{adj}A$ の $ij$ 成分は, $n$ 次正方行列 $A$ の第 $(j,i)$ 余因子 $\widetilde{a}_{ji}$ なので, 右辺の行列積を計算することで \[ x_i = \dfrac{1}{\det A}\displaystyle\sum_{j=1}^n\widetilde{a}_{ji}b_j \] が得られる. 一方で, $A$ の第 $i$ 列を $\mathbf{b}$ に置き換えた行列 $A_i$ の余因子展開より \[ \det A_i = \sum_{j=1}^n b_{j}\widetilde{a}_{ji} \] である. 上 $2$ つの式を組み合わせることで, \[ x_i = \dfrac{\det A_i}{\det A} \] が示される.

\[ A = \begin{pmatrix} a & b \cr c & d \end{pmatrix},\quad \mathbf{x} = \begin{pmatrix} x_1 \cr x_2 \end{pmatrix},\quad \mathbf{b} = \begin{pmatrix} e \cr f \end{pmatrix}. \]

$\det A = ad-bc\neq0$ のとき, 連立 $1$ 次方程式 \[ A\mathbf{x}=\mathbf{b} \] を, クラメルの公式を用いて解いてみよう.
行列 $A$ の第 $i$ 列を $\mathbf{b}$ に置き換えた行列を $A_i$ とする, つまり \[ A_1 = \begin{pmatrix} e & b \cr f & d \end{pmatrix},\quad A_2 = \begin{pmatrix} a & e \cr c & f \end{pmatrix}. \]
クラメルの公式より, 連立 $1$ 次方程式の解 $\mathbf{x}$ の第 $i$ 成分はそれぞれ \[ x_1 = \dfrac{\det A_1}{\det A} = \dfrac{de-bf}{ad-bc}, \] \[ x_2 = \dfrac{\det A_2}{\det A} = \dfrac{af-ce}{ad-bc} \] である.
実際に, この $\mathbf{x}$ に対して $A\mathbf{x} = \mathbf{b}$ が成立することを確かめてみよう. 右辺の行列積を計算すると, \[ \begin{array}{rl} A\mathbf{x} &= \begin{pmatrix} a & b \cr c & d \end{pmatrix}\begin{pmatrix} (de-bf) / (ad-bc) \cr (af-ce) / (ad-bc) \end{pmatrix} \cr &= \dfrac{1}{ad-bc}\begin{pmatrix} ade-abf+abf-bce \cr cde-bcf+adf-cde \end{pmatrix} \cr &= \dfrac{1}{ad-bc}\begin{pmatrix} (ad-bc)e \cr (ad-bc)f \end{pmatrix} \cr &= \begin{pmatrix} e \cr f \end{pmatrix} \cr &= \mathbf{b} \end{array} \] を確認できる.

クラメルの公式は, 掃き出し法 (ガウスの消去法) と比較して, 行列の成分が文字で表現されている場合に有用である. 一方で, 具体的な数値を成分とする行列に対する連立 $1$ 次方程式の解法としては, 掃き出し法の方が便利だろう.

まとめ

行列式の定義と性質を紹介し, また行列式の具体的な計算方法や, 行列式の応用した逆行列の計算方法と連立 $1$ 次方程式の解法 (クラメルの公式) を紹介した.

行列式の定義については, 置換という概念が突然現れることや, 数式で表すと複雑な形になることからよくわからないという印象を持つかもしれない. ただし, この定義の意味するものは (面倒ではあるものの) 難解なものではないし, 実際に $2$ 次正方行列や $3$ 次正方行列の場合は簡単に計算できるものである. 最低でも, $2$ 次および $3$ 次正方行列の行列式の定義は (公式として暗記してでも) 利用できるようになるべきだろう.

また, 行列式を計算する方法として余因子展開を, 余因子行列を応用した逆行列や連立 $1$ 次方程式の計算方法としてクラメルの公式を紹介した. 実際には, 成分が数値で与えられた行列に対しては, 行列式を計算する際は行列サイズ削減を, 逆行列や連立 $1$ 次方程式の計算には掃き出し法 (ガウスの消去法) を利用した方が簡単である. 一方で, 成分に文字が含まれている状況では, 余因子展開やクラメルの公式が便利である. 以下の練習問題などで, これらを応用した計算を試してみて欲しい.

練習問題

次の行列式を計算せよ: \[ \det\begin{pmatrix} 0 & -1 & 3 & -4 \cr 1 & 5 & -8 & -1 \cr -1 & -5 & 9 & -1 \cr -1 & -4 & -2 & 7 \end{pmatrix}. \]

次の行列式を計算せよ: \[ \det\begin{pmatrix} 0 & a & b & c \cr -a & 0 & d & e \cr -b & -d & 0 & f \cr -c & -e & -f & 0 \end{pmatrix}. \]

次の行列式を計算せよ: \[ \det\begin{pmatrix} 1 & 1 & 1 & 1 \cr a & a & a & y \cr z & c & x & y \cr b & b & x & y \end{pmatrix}. \]

実数 $a$, $b$, $c$, $d$, $e$ に対して, \[ A = \begin{pmatrix} a & 0 & b \cr 0 & c & 0 \cr d & 0 & e \end{pmatrix},\quad \mathbf{x} = \begin{pmatrix} x \cr y \cr z \end{pmatrix},\quad \mathbf{b} = \begin{pmatrix} 1 \cr 1 \cr 1 \end{pmatrix} \] とする.

行列 $A$ を正則にする $a$, $b$, $c$, $d$, $e$ の条件を求めよ.
上の条件が満たされるとき, 連立 $1$ 次方程式 $A\mathbf{x}=\mathbf{b}$ を解け.

解答例