1: 行列
1.1: 行列の定義
ここでは, 行列および行列の演算, 操作について紹介する.
行列を用いることで, 多くの数を同時に扱うことが可能であり, これは例えば連立 $1$ 次方程式の記述や, ベクトルの $1$ 次変換の表現などに応用される. 計算機で取り扱う大量のデータや, 物理現象の記述では変位 (つまり位置) , 運動の向き, 速度といった関連する情報は, しばしばベクトルとして表現される. 従って, 連立 $1$ 次方程式の解としてそれらを求めたり, もしくはそれらを変換する際に行列を頻繁に用いることになる.
行列は, 複数の数を長方形状に並べたものとして表現されるが, 四則演算の定義などに $1$ つの数との類似性が見られ, " $1$ つの数"を拡張した概念だと言うことができるだろう.
- 縦に$m$個, 横に$n$個の数を長方形状に並べたものを$m\times n$ 型の行列 (matrix) という.
- 行列を構成する$m\times n$個の数を行列の成分 (element) という.
- 行列を構成する要素たちを横に並べた部分を行 (row), 縦に並べた部分を列 (column)という.
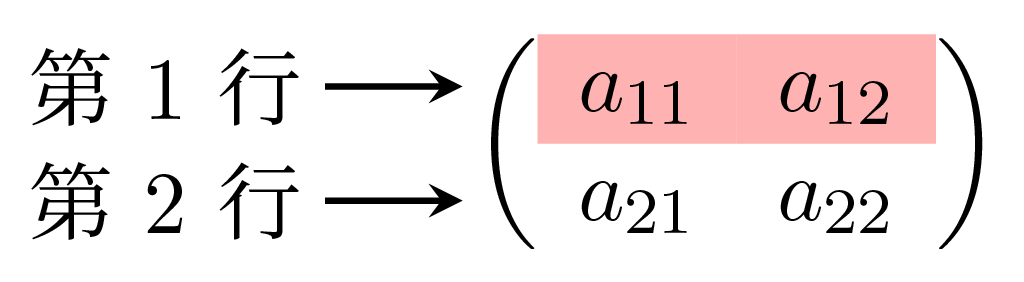
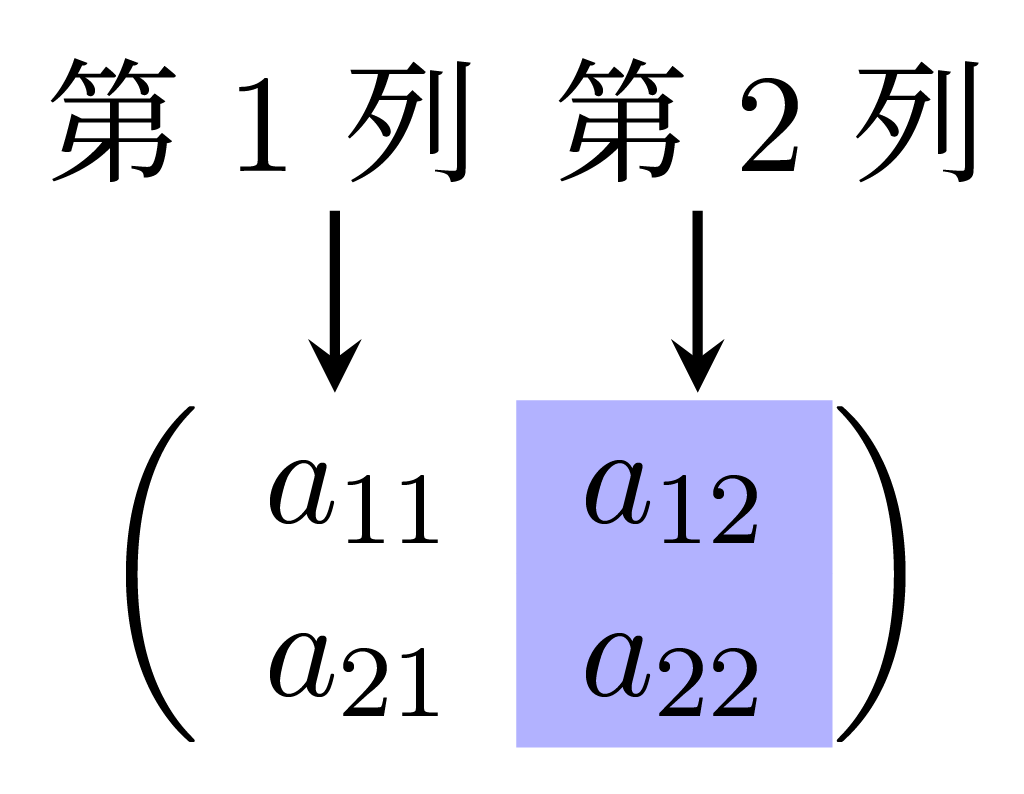
- 上から $i$ 番目の行を第 $i$ 行, 左から $j$ 番目の列を第 $j$ 列という.
- 第 $i$ 行, 第 $j$ 列にある成分を $ (i,j) $ 成分という.
- 以降, 断りの無い限り, 行列は大文字のアルファベットで表記する.
- 行列 $A$ の $(i,j)$ 成分は小文字のアルファベットを用いて $ a_{ij} $ や $a_{i,j}$ と表したり, $A_{ij}$ や $(A)_{ij}$ と表記されることがある.
- また, $(i,j)$ 成分が $a_{ij}$ である行列を $(a_{ij})$ や $(a_{ij})_{1\le i\le m,\ 1\le j\le n}$ などと表すことがある.
- 上と合わせて $A=(a_{ij})$ などと表記することがある.
- 行列 $A$ の第 $1$ 行は $(a_{11},a_{12})$.
- 行列 $A$ の第 $2$ 列は $\begin{pmatrix}a_{12}\cr a_{22}\end{pmatrix}$.
- 行列 $A$ の $(1,2)$ 成分は $a_{12}$.
- 全ての成分が実数である行列を実行列 (real matrix)という.
- 行列 $A$ が $m\times n$ 型の実行列であるとき, $A\in \mathbb{R}^{m\times n}$ と表記する.
- 全ての成分が複素数である行列を複素行列 (complex matrix)という.
- 行列 $A$ が $m\times n$ 型の複素行列であるとき, $A\in \mathbb{C}^{m\times n}$ と表記する.
実数 $a$, $b$, $c$, $d$ に対して,
\[ A = \begin{pmatrix}a&b\cr c&d\end{pmatrix} \]は実行列であり, $A\in\mathbb{R}^{2\times 2}$ である. また, 実数は特に複素数でもあるため, $A\in \mathbb{R}^{2\times 2}\subset \mathbb{C}^{2\times 2}$ である.
- $1\times n$ 型の行列を行ベクトル (row vector) もしくは横ベクトルという.
- 行列 $A\in\mathbb{R}^{m\times n}$ の第 $i$ 行は $1\times n$ 型の行列, つまり行ベクトルになるが, これを $A$ の第 $i$ 行ベクトルという.
- $m\times 1$ 型の行列を列ベクトル (column vector) もしくは縦ベクトルという.
- 行列 $A\in\mathbb{R}^{m\times n}$ の第 $j$ 列は $m\times 1$ 型の行列, つまり列ベクトルになるが, これを $A$ の第 $j$ 列ベクトルという.
- $1\times 1$ 型の行列は, そのただ $1$ つの成分である実数 (もしくは複素数) と同一視される.
- $\mathbf{x} = (x_1,x_2,x_3)\in\mathbb{R}^{1\times3}$ は行ベクトル.
- $\mathbf{v} = \begin{pmatrix}v_1\cr v_2\cr v_3\end{pmatrix}\in\mathbb{R}^{3\times1}$ は列ベクトル.
- $\begin{pmatrix}a\end{pmatrix}\in\mathbb{R}^{1\times1}$ は $a\in\mathbb{R}$ と同一視される.
行ベクトルに限り, この資料では各成分をカンマ (,) で区切って表記することにする.
例えば, 行列
\[ A = \begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n}\cr a_{21}&a_{22}&\dots&a_{2n}\cr \vdots&\vdots&\ddots&\vdots\cr a_{m1}&a_{m2}&\dots&a_{mn} \end{pmatrix} \]の第 $i$ 行ベクトルは
\[ (a_{i1}, a_{i2}, \dots, a_{in}) \]であり, これを $\mathbf{a}_i$ と表すことで
\[ A = \begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n}\cr a_{21}&a_{22}&\dots&a_{2n}\cr \vdots&\vdots&\ddots&\vdots\cr a_{m1}&a_{m2}&\dots&a_{mn} \end{pmatrix} = \begin{pmatrix} \mathbf{a}_1 \cr \mathbf{a}_2 \cr \vdots \cr \mathbf{a}_m \end{pmatrix}. \]と表記することがある. 列ベクトルについても, 同様の表記を用いることがある.
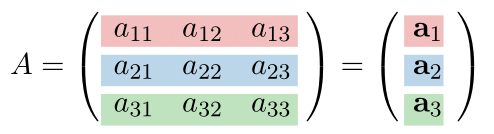
1.2: 行列の演算と操作
ここでは, 行列の和と積 (つまり足し算と掛け算) およびスカラー倍, 転置と呼ばれる操作を紹介する. なお, 定義よりベクトルは行列の特殊な場合であり, 行列に対する演算や操作はベクトルに対しても適用されるものである.
まずは, "$2$ つの行列が等しい"ということの定義を与える:
$2$つの行列 $A=(a_{ij})$, $B=(b_{ij})$ について, $A$ と $B$ が同じ型であって, 全ての $i,j$ に対して \[ a_{ij} = b_{ij} \] となるとき, $A$ と $B$ は等しいといい, \[ A=B \] と表記する. $A=B$ でない場合は, $A\neq B$ と表記する.
- 行列の型が同じで, 全ての成分が等しいため $A=B$.
- $(2,2)$ 成分が異なるため $A\neq C$.
- 行列の型が異なるため $A\neq D$.
行列の和は, 成分ごとに足し合わせることで定義される:
- $A+B = \begin{pmatrix}1&2\cr 3&4\end{pmatrix}+\begin{pmatrix}1&2\cr 3&4\end{pmatrix} = \begin{pmatrix}2&4\cr 6&8\end{pmatrix}.$
- $A+C = \begin{pmatrix}1&2\cr 3&4\end{pmatrix} + \begin{pmatrix}1&2\cr 3&0\end{pmatrix} = \begin{pmatrix}2&4\cr 6&4\end{pmatrix}.$
- 行列の型が異なるため, $A+D$ は定義されない.
定義より次は明らかである:
以下の行列 $A$, $B$ に対し $A+B$ と $B+A$ を計算し, それらが一致することを確認せよ: \[ A = \begin{pmatrix} a & b \cr c & d \end{pmatrix}, \quad B = \begin{pmatrix} e & f \cr g & h \end{pmatrix}. \]
\[ A + B = B + A = \begin{pmatrix} a + e & b + f \cr c + g & d + h \end{pmatrix}. \]
次に, 行列に"$1$ つの数" (これをベクトルと対比してスカラー値と呼ぶ) を掛けるという演算を紹介する.
行列 $A=(a_{ij})$ と複素数 $\lambda$ に対し, $(i,j)$ 成分が $\lambda a_{ij}$ である行列を $\lambda A$ と表記する.
\[ \lambda\begin{pmatrix} a & b \cr c & d \end{pmatrix} = \begin{pmatrix} \lambda a & \lambda b \cr \lambda c & \lambda d \end{pmatrix}. \]
次を計算せよ: \[ 2\begin{pmatrix} 1&2\cr 3&4 \end{pmatrix}-\begin{pmatrix} 4&3\cr 2&0 \end{pmatrix}. \]
\[ 2\begin{pmatrix} 1&2\cr 3&4 \end{pmatrix}-\begin{pmatrix} 4&3\cr 2&0 \end{pmatrix} = 2\begin{pmatrix} 1&2\cr 3&4 \end{pmatrix}+ (-1)\begin{pmatrix} 4&3\cr 2&0 \end{pmatrix} = \begin{pmatrix} 2 & 4 \cr 6 & 8 \end{pmatrix} + \begin{pmatrix} -4 & -3 \cr -2 & 0 \end{pmatrix} = \begin{pmatrix} -2 & 1 \cr 4 & 8 \end{pmatrix}. \]
次に紹介する行列の積は, 初学者には難しく感じられるかもしれないが, 計算できるようになる必要がある.
$\ell\times m$ 型行列 $A=(a_{ij})$と, $m\times n$ 型行列 $B=(b_{ij})$ に対し, $(i,j)$ 成分が \[ \displaystyle\sum_{k=1}^m a_{ik}b_{kj} \] である $\ell \times n$ 型行列を, 行列 $A$ と $B$ の積 (行列積) といい, $AB$ と表記する.
行列積 $AB$ は, 左側の行列 $A$ の列の数と, 右側の行列 $B$ の行の数が等しいときに限り定義される.
行列積は一般には非可換である, つまり一般には $AB\neq BA$ である. また, 行列積 $AB$ が定義されたとしても, 行列積 $BA$ が定義されるとは限らない.
- $\mathbf{x}\mathbf{y}\in\mathbb{R}^{1\times1}$ の $(1,1)$ 成分は $\displaystyle\sum_{k=1}^2 x_ky_k$.
- つまり行列 $\mathbf{x}\mathbf{y}$ は, そのただ $1$ つの成分である $x _ 1y _ 1+x _ 2y _ 2$ と同一視される.
- なお, この形の行列積はベクトル $\vec{x}=(x_1,x_2)$ と $\vec{y}=(y_1,y_2)$ の内積 \[ \vec{x}\cdot\vec{y} = x_1y_1+x_2y_2 \] と一致する.
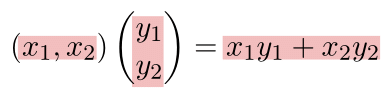
\[ A = \begin{pmatrix} a_{11}&a_{12}\cr a_{21}&a_{22} \end{pmatrix},\quad B = \begin{pmatrix} b_{11}&b_{12}\cr b_{21}&b_{22} \end{pmatrix} \]
- $AB = \begin{pmatrix} a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}\cr a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22} \end{pmatrix}.$
- 行列 $AB$ の $(i,j)$ 成分は, $A$ の第 $i$ 行ベクトル $\mathbf{a}_i$ と $B$ の第 $j$ 列ベクトル $\mathbf{b}_j$の積となる; \[ AB = \begin{pmatrix} \mathbf{a}_1\mathbf{b}_1&\mathbf{a}_1\mathbf{b}_2\cr \mathbf{a}_2\mathbf{b}_1&\mathbf{a}_2\mathbf{b}_2 \end{pmatrix}, \] ここで $\mathbf{a}_i = (a_{i1},a_{i2})$, $\mathbf{b}_j = \begin{pmatrix} b_{1j}\cr b_{2j} \end{pmatrix}$ である.
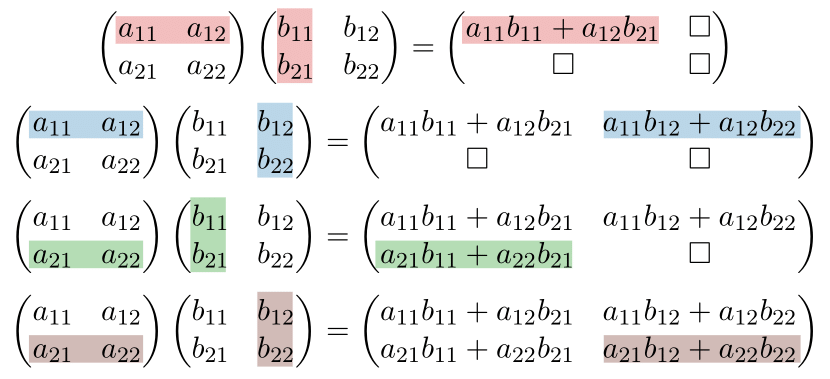
\[ A = \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix},\quad \mathbf{x} = \begin{pmatrix} x_1\cr x_2 \end{pmatrix}. \]
- $A{\boldsymbol{x}} = \begin{pmatrix}x_1+2x_2\cr 3x_1+4x_2\end{pmatrix}$.
- このように, 行列と列ベクトルの積により列ベクトルが得られる.
- 実は連立 $1$ 次方程式は, 『与えられた行列 $A$ と列ベクトル ${\boldsymbol{b}}$ に対し, $A{\boldsymbol{x}} = {\boldsymbol{b}}$ を満たす列ベクトル ${\boldsymbol{x}}$ を求めよ』 という形で表記することができる. これは行列の重要な応用の $1$ つである.
\[ \mathbf{x} = (x_1,x_2)\in\mathbb{R}^{1\times2},\quad \mathbf{y} = \begin{pmatrix} y_1\cr y_2 \end{pmatrix}\in\mathbb{R}^{2\times1}. \]
- いま, \[ \mathbf{y}\mathbf{x} = \begin{pmatrix} y_1x_1&y_1x_2\cr y_2x_1&y_2x_2 \end{pmatrix}\in\mathbb{R}^{2\times 2} \] であり, これはベクトルの内積と一致しない.
- ベクトルの内積と一致するのは, $(\text{行ベクトル})(\text{列ベクトル})$ という形をしたベクトル同士の行列積であり, 上のように $(\text{列ベクトル})(\text{行ベクトル})$ という形の積に関してはこの限りでは無い.
- ちなみに, $2$ つのベクトルに対するこの形の積は テンソル積 と呼ばれるものの一種であり, 特に 直積 もしくは 外積 (outer product) と呼ばれる.
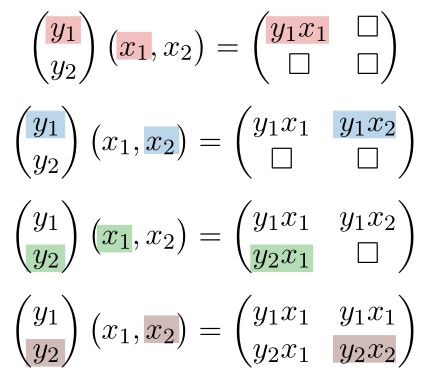
以下の行列 $A$, $B$ に対し, $AB$ と $BA$ を計算し, それらが一致しないことを確認せよ: \[ A = \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix},\quad B = \begin{pmatrix} 2&3\cr 4&5 \end{pmatrix}. \]
- $AB = \begin{pmatrix}
1\cdot2+2\cdot4 & 1\cdot3+2\cdot5\cr
3\cdot2+4\cdot4 & 3\cdot3+4\cdot5
\end{pmatrix}$
$\hspace{30px} = \begin{pmatrix} 10&13\cr 22&29 \end{pmatrix}.$ - $BA = \begin{pmatrix}
2\cdot1+3\cdot3 & 2\cdot2+3\cdot4\cr
4\cdot1+5\cdot3 & 4\cdot2+5\cdot4
\end{pmatrix}$
$\hspace{30px} = \begin{pmatrix} 11&16\cr 19&28 \end{pmatrix}.$
以下の行列 $A$, $B$ に対して, 行列積 $AB$, $BA$ は定義されるか. 定義されるなら行列積の計算結果を求め, 定義されないならば "定義されない" と答えよ: \[ A = \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix},\quad B = \begin{pmatrix} 2&3&0\cr 4&5&0 \end{pmatrix}. \]
- 行列積 $AB$ を考えると, 左側の行列 $A$ の列の数は$2$, 右側の行列 $B$ の行の数は $2$ で等しいため, 行列積 $AB$ は定義される. 実際に計算すると \[ AB = \begin{pmatrix} 10&13&0\cr 22&29&0 \end{pmatrix} \] となる.
- 一方, 行列積 $BA$ を考えると, $B$ の列の数は$3$, $A$ の行の数は $2$ で異なっているため, 行列積 $BA$ は定義されない.
$2$ つの行列 \[ A = \begin{pmatrix} a & 1 \cr 0 & b \end{pmatrix},\quad B = \begin{pmatrix} c & 1 \cr 0 & d \end{pmatrix} \] に対して, $AB=BA$ とする $a, b, c, d$ を求めよ.
\[ AB = \begin{pmatrix} ac & a+d \cr 0 & bd \end{pmatrix},\quad BA = \begin{pmatrix} ac & b+c \cr 0 & bd \end{pmatrix} \] より, $a+d=b+c$ を満たす全ての $a,b,c,d$ に対して $AB=BA$ が成立する.
以下の $2$ つの性質は, "$1$ つの数"に対しても成立するものであるが, 行列に対しても同様に成り立つ:
行列 $A$, $B$, $C$ がそれぞれ $k\times\ell$ 型, $\ell\times m$ 型, $m\times n$ 型であるならば, \[ (AB)C = A(BC) \] が成立する.
$A=(a_{ip})$, $B=(b_{pq})$, $C=(c_{qj})$ とする. 行列 $(AB)\in\mathbb{R}^{k\times m}$ の $(i,q)$ 成分は \[ \displaystyle\sum_{p=1}^{\ell} a_{ip}b_{pq} \] なので, 行列 $(AB)C$ の $(i,j)$ 成分は \[ \displaystyle\sum_{q=1}^m\left(\sum_{p=1}^{\ell}a_{ip}b_{pq}\right) c_{qj} = \sum_{p=1}^{\ell}\sum_{q=1}^ma_{ip}b_{pq}c_{qj} \] となる.
一方で, 行列 $(BC)\in\mathbb{R}^{\ell\times n}$ の $(p,j)$ 成分は \[ \sum_{q=1}^mb_{pq}c_{qj} \] なので, 行列 $A(BC)$ の $(i,j)$ 成分は \[ \sum_{p=1}^{\ell}a_{ip}\left(\sum_{q=1}^mb_{pq}c_{qj}\right) = \sum_{p=1}^{\ell}\sum_{q=1}^ma_{ip}b_{pq}c_{qj} \] となる. 従って, $(AB)C = A(BC)$ が得られる.
- 行列 $A$, $B$, $C$ がそれぞれ $\ell\times m$ 型, $m\times n$ 型, $m\times n$ 型であるならば, \[ A(B+C) = AB+AC \] が成立する.
- 行列 $A$, $B$, $C$ がそれぞれ $\ell\times m$ 型, $\ell\times m$ 型, $m\times n$ 型であるならば, \[ (A+B)C = AC+BC \] が成立する.
複素行列 (特に各成分が実数でない場合) に対しては, 各成分の複素共役 (虚部の符号が反転したもの) をとることがある:
行列 $A$ の各成分を, その複素共役で置き換えた行列を複素共役行列といい, $\overline{A}$ と表記する.
定義より次は明らかである:
- $\overline{\overline{A}}=A,$
- $\overline{A+B} = \overline{A}+\overline{B},$
- $\overline{\lambda A} = \overline{\lambda}\ \overline{A},$
- $\overline{AB} = \overline{A}\ \overline{B}.$
次に, 行列の転置という操作を紹介しよう. これは, 行列の行と列を入れ替える操作であり, "$1$ つの数" (実数や複素数) には無い行列に特有のものである:
行列 $A=(a_{ij})$ に対し, 第 $(i,j)$ 成分が $a_{ji}$ である行列を $A$ の転置行列 (もしくは単に転置) といい, $A^{\operatorname{T}}$ (もしくは ${}^tA$) と表記する. 行列の転置行列をとる操作を転置 (transpose) という.
- 転置は行と列を入れ替える (つまり $i$ と $j$ を入れ替える) 操作である.
- $m\times n$ 型行列の転置は $n\times m$ 型行列になる.
- 特に, 列ベクトルの転置は行ベクトルになり, 行ベクトルの転置は列ベクトルになる.
- $\mathbf{x} = (x_1,x_2)$ のとき, $\mathbf{x}^{\operatorname{T}} = \begin{pmatrix} x_1\cr x_2 \end{pmatrix}$.
- $A = \begin{pmatrix} a_{11}&a_{12}\cr a_{21}&a_{22} \end{pmatrix}$ のとき, $A^{\operatorname{T}} = \begin{pmatrix} a_{11}&a_{21}\cr a_{12}&a_{22} \end{pmatrix}$.
- $B = \begin{pmatrix} b_{11}&b_{12}&b_{13}\cr b_{21}&b_{22}&b_{23} \end{pmatrix}$ のとき, $B^{\operatorname{T}} = \begin{pmatrix} b_{11}&b_{21}\cr b_{12}&b_{22}\cr b_{13}&b_{23} \end{pmatrix}$.
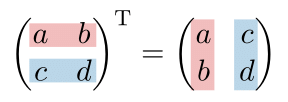
- $(A^{\operatorname{T}})^{\operatorname{T}}=A,$
- $(A+B)^{\operatorname{T}} = A^{\operatorname{T}}+B^{\operatorname{T}},$
- $(AB)^{\operatorname{T}} = B^{\operatorname{T}}A^{\operatorname{T}}.$
$(AB)^{\operatorname{T}} = B^{\operatorname{T}}A^{\operatorname{T}}$ のみ証明する: $A=(a_{ik})\in\mathbb{R}^{\ell\times m}$, $B=(b_{kj})\in\mathbb{R}^{m\times n}$ とすると, $(AB)^{\operatorname{T}}$ の $(i,j)$ 成分は行列 $AB$ の $(j,i)$ 成分に等しいため \[ \sum_{k=1}^ma_{jk}b_{ki} \] である. 一方, $B^{\operatorname{T}}$ の第 $i$ 行ベクトルは, $B$ の第 $i$ 列ベクトル $\mathbf{b}_i$ の転置であり, $A^{\operatorname{T}}$ の第 $j$ 列ベクトルは, $A$ の第 $j$ 行ベクトル $\mathbf{a}_j$ の転置である. 従って, 行列 $B^{\operatorname{T}} A^{\operatorname{T}}$ の $(i,j)$ 成分は \[ \begin{array}{rl} \mathbf{b}_i^{\operatorname{T}}\mathbf{a}_j^{\operatorname{T}} &= \begin{pmatrix}b_{1i}, b_{2i}, \dots, b_{mi}\end{pmatrix} \begin{pmatrix} a_{j1}\cr a_{j2}\cr \vdots\cr a_{jm} \end{pmatrix} \cr & = \displaystyle\sum_{k=1}^m a_{jk} b_{ki}. \end{array} \] これが任意の $i$, $j$ に対して成立するため, $2$ つの行列 $(AB)^{\operatorname{T}}$ と $B^{\operatorname{T}}A^{\operatorname{T}}$ の全ての成分は等しい, つまり $(AB)^{\operatorname{T}} = B^{\operatorname{T}}A^{\operatorname{T}}$ が成立する.
以下の行列 $A$, $B$ に対して, $AB$ と $B^{\operatorname{T}}A^{\operatorname{T}}$ を計算し, $(AB)^{\operatorname{T}} = B^{\operatorname{T}}A^{\operatorname{T}}$ を確認せよ: \[ A = \begin{pmatrix} 1&2&3\cr 4&5&6 \end{pmatrix},\quad B=\begin{pmatrix} 2&4\cr 6&8\cr 10&12 \end{pmatrix}. \]
- $AB = \begin{pmatrix} 44& 56\cr 98&128 \end{pmatrix}$.
- $A^{\mathrm{T}} = \begin{pmatrix} 1&4\cr 2&5\cr 3&6 \end{pmatrix}$, $B^{\operatorname{T}} = \begin{pmatrix} 2&6&10\cr 4&8&12 \end{pmatrix}$.
- $B^{\operatorname{T}}A^{\operatorname{T}} = \begin{pmatrix} 44&98\cr 56&128 \end{pmatrix} = (AB)^{\operatorname{T}}$.
1.3: 正方行列など
ここでは, 特定の性質を満たす行列の名称や表記と, その性質を紹介する.
全ての成分が $0$ である行列を零行列 (zero matrix) といい, $O$ と表記する.
- $O = \begin{pmatrix}0\end{pmatrix}\in\mathbb{R}^{1\times 1}$. これは $0\in\mathbb{R}$ と同一視される.
- $O=\begin{pmatrix}0&0\cr 0&0\end{pmatrix}\in\mathbb{R}^{2\times 2}$.
任意の行列 $A$ に対して, 以下が成立する:
- $A-A = O$. この $O$ は $A$ と同じ型になる.
- $A+O = A$, ただし $A$ と $O$ は同じ型とする.
- $0A =O$, この $O$ は $A$ と同じ型になる.
- 行列積 $AO$ が定義されるなら $AO=O$, ただし両辺の $O$ が同じ型とは限らない.
- 行列積 $OA$ が定義されるなら $OA=O$, ただし両辺の $O$ が同じ型とは限らない.
- $(A-A)\mathbf{x} = \begin{pmatrix} 0&0\cr 0&0 \end{pmatrix}\mathbf{x} = \mathbf{0}$.
- $A(\mathbf{x}-\mathbf{x}) = A\mathbf{0} = \mathbf{0}$.
$m\times n$ 型の行列 $A$ について, $m=n$ であるとき (つまり行と列の数が等しいとき) $A$ を正方行列 (square matrix), もしくは $n$ 次正方行列という.
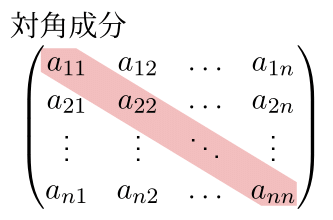
- $A=(a_{ij})$ が正方行列ならば, $A$ の成分 $a_{ii}$ たちは行列の左上から右下にかけての対角線上に位置している. これらの成分を対角成分 (main diagonal) という.
- 正方行列 $A$ の転置行列 $A^{\mathrm{T}}$ は $A$ と同じ型の正方行列となり, それらの対角成分は一致する.
- $A$ が正方行列ならば, 行列積 $AA$ が定義できる. これを $A^2$ と表記する.
- 同様に, $k$ 個の $A$ を掛け合わせた行列積 $A\cdots A$ を $A^k$ と表記する.
正方行列 $A$ について, \[ A=A^{\mathrm{T}} \] が成立するとき, $A$ を対称行列 (symmetric matrix) という.
行列 $A$ の転置 $A^{\mathrm{T}}$ の定義より, 正方行列 $A = (a_{ij})$ が対称行列であることは, 任意の $i$, $j$ に対して \[ a_{ij} = a_{ji} \] が成立することと同値である.
正方行列 $A$ について, \[ A=-A^{\mathrm{T}} \] が成立するとき, $A$ を歪対称行列 (skew-symmetric matrix) もしくは交代行列 (alternating matrix) という.
- 正方行列 $A = (a_{ij})$ が歪対称であることは, 任意の $i$, $j$ に対して \[ a_{ij} = -a_{ji} \] が成立することと同値である.
- 正方行列 $A=(a_{ij})$ が歪対称行列ならば, 特に任意の $i$ に対して $a_{ii} = -a_{ii}$, すなわち \[ a_{ii}=0 \] が成立する. つまり, 歪対称行列の対角成分は必ず $0$ である.
正方行列 $A$ について, その対角成分以外が $0$ であるとき, $A$ を対角行列 (diagonal matrix) という.
- $A = \begin{pmatrix} a_1&0&0\cr 0&a_2&0\cr 0&0&a_3 \end{pmatrix}$ は正方行列であり, 非対角成分が全て $0$ なので対角行列である.
- 全ての対角行列は対称行列でもある.
- 以降, \[ \delta_{ij} = \left\lbrace\begin{array}{rll} 1 &\text{if } i=j,\cr 0 &\text{if } i\neq j \end{array}\right. \]という表記を用いることがある (これをクロネッカーのデルタ記号, Kronecker delta という). これを用いると, 対角行列は \[ A = (a_i\delta_{ij}) \] と表記できる.
対角成分が全て $1$ である対角行列を単位行列 (identity matrix) といい, $I$ ( もしくは $E$ ) と表記する.
- $I = \begin{pmatrix}1\end{pmatrix}\in\mathbb{R}^{1\times 1}$. これは $1\in\mathbb{R}$ と同一視される.
- $I=\begin{pmatrix}1&0\cr 0&1\end{pmatrix}\in\mathbb{R}^{2\times2}$.
- $I=\begin{pmatrix}1&0&0\cr 0&1&0\cr 0&0&1\end{pmatrix}\in\mathbb{R}^{3\times 3}$
- 特に $n$ 次正方行列である単位行列を $I_n$ ( もしくは $E_n$ ) と表記することがある.
- クロネッカーのデルタを用いると, $I=(\delta_{ij})$ と表記できる.
- 全ての対角成分が $\lambda$ である対角行列は $\lambda I$ と表すことができる.
この行列を"単位"行列と呼ぶのは, 以下の性質が成り立つからである:
- 行列積 $IA$ が定義されるなら $IA=A$.
- 行列積 $AI$ が定義されるなら $AI=A$.
- 任意の $k$ に対し, $I^k=I$.
証明略.
単位行列に関連して, 以下にも言及しておく:
行列積の定義で述べたように, 行列積 $AB$ の $(i,j)$ 成分 は $A$ の第 $i$ 行ベクトルと $B$ の第 $j$ 列ベクトルの行列積を用いて表現することができる. これを一般化してブロック行列 (block matrix) もしくは行列の区分け (partitioning) による行列積の表現が可能である.
- 行列 $A$ の第 $j$ 列を $\mathbf{a}_j$ とすると, $A=\left(\begin{array}{c:c} \mathbf{a}_1 & \mathbf{a}_2 \end{array}\right)$ という区分けが得られる.
- このとき, \[ \begin{array}{rl} A\mathbf{x} &= (\mathbf{a}_1, \mathbf{a}_2)\begin{pmatrix} x \cr y \end{pmatrix} \cr &= \mathbf{a}_1x + \mathbf{a}_2y \end{array} \] という表記が得られる. 実際, \[ \begin{array}{rl} \mathbf{a}_1x + \mathbf{a}_2y &= \begin{pmatrix} a_{11} \cr a_{21} \end{pmatrix}x + \begin{pmatrix} a_{12} \cr a_{22} \end{pmatrix}y \cr &= \begin{pmatrix} a_{11}x + a_{12}y \cr a_{21}x + a_{22}y \end{pmatrix} \end{array} \] であり, 区分けを用いず $A\mathbf{x}$ を計算したときと同じ結果が得られることを確認できる.
標準基底 $\mathbf{e}_1, \mathbf{e}_2\in\mathbb{R}^2$ に対して, \[ A\mathbf{e}_1 = \begin{pmatrix} a \cr b \end{pmatrix}, \quad A\mathbf{e}_2 = \begin{pmatrix} c \cr d \end{pmatrix} \] を満たす $A\in\mathbb{R}^{2\times 2}$ を求めよう. ブロック行列を用いた表記により \[ A = AI = A\left( \mathbf{e}_1, \mathbf{e}_2 \right) = \left(\begin{array}{c:c} a & c \cr b & d \end{array}\right) \] が得られるため, \[ A = \begin{pmatrix} a & c \cr b & d \end{pmatrix} \] である.
以下を計算せよ: \[ \begin{pmatrix} 1 & 2 & 0 & 0 \cr 3 & 4 & 0 & 0 \cr 0 & 0 & 1 & 2 \cr 0 & 0 & 3 & 4 \end{pmatrix}^2. \]
\[ A = \begin{pmatrix} 1 & 2 \cr 3 & 4 \end{pmatrix} \] とおくと, \[ \begin{pmatrix} 1 & 2 & 0 & 0 \cr 3 & 4 & 0 & 0 \cr 0 & 0 & 1 & 2 \cr 0 & 0 & 3 & 4 \end{pmatrix}^2 = \begin{pmatrix} A & O \cr O & A \end{pmatrix}^2 = \begin{pmatrix} A^2 & O \cr O & A^2 \end{pmatrix} = \begin{pmatrix} 7 & 10 & 0 & 0 \cr 15 & 22 & 0 & 0 \cr 0 & 0 & 7 & 10 \cr 0 & 0 & 15 & 22 \end{pmatrix}. \]
次に述べる逆行列は, 行列の"割り算"に相当するものであり非常に重要である.
正方行列 $A$ に対して, 同じ型の正方行列 $B$ であって \[ AB = BA = I \] を満たすものが存在するならば, $B$ を $A$ の逆行列 (inverse matrix) といい, $B=A^{-1}$ と表記する. 正方行列 $A$ の逆行列が存在するならば, $A$ を正則行列 (regular matrix) もしくは可逆行列 (invertible matrix) という.
- 零行列 $O\in\mathbb{R}^{n\times n}$ の逆行列は存在しない.
- 単位行列 $I$ の逆行列は単位行列 $I$ である: $I^{-1}=I$.
- 対角行列 \[ A = \begin{pmatrix}a_1&0&\dots&0\cr 0&a_2&\dots&0\cr \vdots&\vdots&\ddots&\vdots\cr 0&0&\dots&a_n\end{pmatrix} \] は, 任意の $i$ に対し $a_i\neq0$ が成立するならば正則行列であり, 逆行列は \[ A^{-1} = \begin{pmatrix}1/a_1&0&\dots&0\cr 0&1/a_2&\dots&0\cr \vdots&\vdots&\ddots&\vdots\cr 0&0&\dots&1/a_n\end{pmatrix} \] である.
- $A=\begin{pmatrix} 1&2\cr 3&4 \end{pmatrix}$ とする. いま, \[ A\begin{pmatrix} -2&1\cr 3/2&-1/2 \end{pmatrix} = I, \] \[\begin{pmatrix} -2&1\cr 3/2&-1/2 \end{pmatrix}A = I \] が成立するので, $A^{-1} = \begin{pmatrix} -2&1\cr 3/2&-1/2 \end{pmatrix}$.
- $B = \begin{pmatrix} 1&2\cr 2&4 \end{pmatrix}$ の逆行列は存在しない. これは背理法で以下のように確かめられる: もしも \[ B\begin{pmatrix} a&b\cr c&d \end{pmatrix} = I \] を満たす行列 $\begin{pmatrix} a&b\cr c&d \end{pmatrix}$ が存在したならば, \[ \left\lbrace\begin{array}{rl} a+2c &= 1,\cr b+2d &= 0,\cr 2a+4c &= 0,\cr 2b+4d &= 1 \end{array}\right. \] となり矛盾する.
逆行列について以下が成立する:
- $A^{-1}$ が存在するならば, $(A^{-1})^{-1} = A$.
- $A^{-1}$ は存在するならばただ$1$つに定まる.
- 同じ型の正方行列 $A$, $B$ に対し, $A^{-1}$, $B^{-1}$ が存在するならば $(AB)^{-1} = B^{-1}A^{-1}$.
- 逆行列の定義より $A^{-1}$ は \[ AA^{-1} = A^{-1}A = I \] を満たす. ここで, もう一度逆行列の定義を使うと $A$ は $A^{-1}$ の逆行列である, つまり $(A^{-1})^{-1}=A$ である.
- (背理法) $2$ つの異なる行列 $B$, $C$ に対して, \[ AB=BA=I, \] \[ AC=CA=I \] が成立すると仮定する. このとき, 行列積の結合則 より \[ B = BI = B(AC) = (BA)C = IC = C \] となるが, これは $B\neq C$ に矛盾する. 従って, 背理法より $A$ の逆行列はただ $1$ つに定まる.
- 行列 $AB$ と $(B^{-1}A^{-1})$ について, 行列積の結合則より \[ \begin{array}{rl} (AB)(B^{-1}A^{-1}) &= A(BB^{-1})A^{-1} \cr &= AIA^{-1} \cr &= AA^{-1}=I, \end{array} \] \[ \begin{array}{rl} (B^{-1}A^{-1})(AB) &= B^{-1}(A^{-1}A)B \cr &= B^{-1}IB \cr &= B^{-1}B=I. \end{array} \] 逆行列の定義より $(AB)^{-1} = B^{-1}A^{-1}.$
- 上の結果より, 特に正則行列たちの積は正則行列になる.
- 実は, 正方行列 $A$ に対し $AB=I$ を満たす $B$ が存在すれば, そのような $B$ は $BA=I$ も満たす (つまり $B=A^{-1}$ となる).
- 同様に, $BA=I$ なる $B$ は, $B=A^{-1}$ となる.
- いま, $AB = I$ となることだけ確かめれば, 実は $BA=I$ も満たされるため, $B=A^{-1}$ であることがわかる.
- 同様に $BA=I$ となることだけ確かめれば, 実は $AB=I$ も満たされるため, $B=A^{-1}$ であることがわかる.
正則行列 $A$ に対して, \[ (A^{\operatorname{T}})^{-1} = (A^{-1})^{\operatorname{T}} \] を証明せよ.
わかりやすさのため, \[ B = A^{\operatorname{T}},\quad C = (A^{-1})^{\operatorname{T}} \] とおいてみよう. このとき, $B^{-1}=C$ であることを示せば良い. そのためには, \[ BC = I \quad (\text{もしくは }CB = I) \] であることが確かめられれば良い. ここでは $BC=I$, つまり \[ A^{\operatorname{T}}(A^{-1})^{\operatorname{T}} = I \] であることを証明しよう. 転置の性質を用いると \[ \begin{array}{rl} A^{\operatorname{T}}(A^{-1})^{\operatorname{T}} &= (A^{-1}A)^{\operatorname{T}} \cr &= I^{\operatorname{T}} =I \end{array} \] であることが確かめられる.
まとめ
行列とは何かを説明し, 行列の演算や操作 (和, 差, スカラー倍, 行列積, 転置など) について紹介した. また, 行列演算および操作の性質と, いくつかの特別な行列について紹介した.
特に, 行列の演算については, 実数 (複素数) の演算と同様の性質が成り立つ: 例えば実数に対して \[ \begin{array}{c} a+b = b+a,\quad (ab)c = a(bc),\cr a\times 0 = 0\times a = 0,\quad a\times 1 = 1\times a = a, \cr a^{-1} \text{ が存在するならば } a\times a^{-1} = a^{-1}\times a = 1 \end{array} \] が成り立つが, 行列に対しても同様に \[ \begin{array}{c} A+B = B+A, \quad (AB)C = A(BC), \cr AO = OA = O,\quad AI = IA = A, \cr A^{-1} \text{ が存在するならば } AA^{-1} = A^{-1}A = I \end{array} \] が成立することを紹介した. ただし, 行列の場合は, 型が適切でなければ行列の和や積は定義できないこと, 行列積の交換はできないこと (一般には $AB\neq BA$ であること), 転置のような行列特有の操作があることなどに注意が必要である. また, 実数 $a$ の逆数 $a^{-1}$ が存在する必要十分条件は $a\neq0$ であるが, 正方行列 $A$ に対し逆行列 $A^{-1}$ が存在する (つまり $A$ が正則である) 必要十分条件についてはまだ紹介していない.
逆行列が存在する必要十分条件, および与えられた行列に対する逆行列の計算方法について説明することは, この資料全体を通じての大きなテーマの一つであり, 以降複数の章において言及する.
練習問題
次を単位行列にする $a$, $b$, $c$, $d$ を求めよ: \[ \begin{pmatrix} 2 & -1 & a \cr 0 & b & 4 \cr 1 & 0 & c \end{pmatrix} + \begin{pmatrix} -1 & 1 & 2 \cr 0 & 3 & d \cr -1 & 0 & 0 \end{pmatrix}. \]
次を歪対称行列にする $a$, $b$, $c$, $d$ を求めよ: \[ \begin{pmatrix} 0 & -6a+4c+3 & 2b+3 \cr 3a-2c-12 & d+6 & 1 \cr b & -3a+4c-22 & 0 \end{pmatrix}. \]
$2$ つの正方行列 \[ A = \begin{pmatrix} 1 & a \cr b & c \end{pmatrix},\quad B = \begin{pmatrix} -3 & d \cr 2 & -1 \end{pmatrix} \] に対して, $B=A^{-1}$ とする $a$, $b$, $c$, $d$ を求めよ.