2: 行列の基本変形と応用
2.1: 導入
例として, 以下の連立$1$次方程式を考える: \[ \left\lbrace\begin{array}{rll} x+y &= 5, &(1) \cr 2x+3y &= 13. &(2) \end{array}\right. \] この連立$1$次方程式は, 例えば $(2)$ 式に $(1)$ 式の $-2$ 倍を加えることで $(1)$ 式から $y$ の項を消去する, といった操作 (いわゆる変数消去) を用いて解くことができる. 実際に変数消去を用いて, \[ \begin{array}{rl} &\left\lbrace\begin{array}{rll} x+y &= 5, &(1) \cr 2x+3y &= 13. &(2) \end{array}\right. \cr \leadsto & \left\lbrace\begin{array}{rll} x+y &= 5, &(1)\cr y &= 3. &(2)^\prime = (2) - 2\times (1) \end{array}\right. \cr \leadsto & \left\lbrace\begin{array}{rll} x &= 2, &(1)^\prime = (1) - (2)^\prime\cr y &= 3. &(2)^\prime \end{array}\right. \end{array} \] と変形して, $x=2$, $y=3$ を得ることができる.
一方で, この連立$1$次方程式はベクトルを用いると (行列の等号より) 以下のように表現することができる: \[ \begin{pmatrix} x+y \cr 2x + 3y \end{pmatrix} = \begin{pmatrix} 5 \cr 13 \end{pmatrix}. \] さらに, 左辺のベクトルは行列積を用いて表すことができるため, 以下の方程式は元の連立 $1$ 次方程式と同じものになる: \[ \begin{pmatrix} 1&1\cr 2&3 \end{pmatrix}\begin{pmatrix} x\cr y \end{pmatrix} = \begin{pmatrix} 5\cr 13 \end{pmatrix}. \] ここで, \[ A = \begin{pmatrix} 1&1\cr 2&3 \end{pmatrix},\quad \mathbf{x} = \begin{pmatrix} x \cr y \end{pmatrix},\quad \mathbf{b} = \begin{pmatrix} 5 \cr 13 \end{pmatrix} \] とすると, 最初の連立 $1$ 次方程式は対応する行列 $A$ と列ベクトル $\mathbf{b}$ を用いて, 「$A\mathbf{x} = \mathbf{b}$ を満たす列ベクトル $\mathbf{x}$ を求めよ」 という問題と同一視することができる (この同一視に基づき, 「$A\mathbf{x} = \mathbf{b}$ を満たす列ベクトル $\mathbf{x}$ を求めよ」という問題も連立 $1$ 次方程式と呼ぶことにする). これは行列の基本的な応用の $1$ つである.
いま, \[ B = \begin{pmatrix} 3 & -1 \cr -2 & 1 \end{pmatrix} \] とすると, $AB = I$ を確かめることができるため $B=A^{-1}$ である (参照). これを用いると, \[ \begin{array}{rl} \mathbf{x} &= I\mathbf{x} \cr &= A^{-1}A\mathbf{x} \cr &= A^{-1}\mathbf{b} \cr &= \begin{pmatrix} 3&-1\cr -2&1 \end{pmatrix}\begin{pmatrix} 5 \cr 13 \end{pmatrix} \cr &= \begin{pmatrix} 2\cr 3 \end{pmatrix} \end{array} \] と計算することで, 連立$1$次方程式を解くことができる. すなわち, 行列 $A$ の逆行列を求めることは, 連立 $1$ 次方程式の解法の一つである.
ところで, 変数消去を用いた計算の際は, 例えば $(2)$ 式に $(1)$ 式の $-2$ 倍を加える, といった操作により \[ \begin{array}{rl} &\left\lbrace\begin{array}{rll} x+y &= 5, &(1) \cr 2x+3y &= 13. &(2) \end{array}\right. \cr \leadsto & \left\lbrace\begin{array}{rll} x+y &= 5, &(1)\cr y &= 3. &(2)^\prime = (2) - 2\times (1) \end{array}\right. \cr \leadsto & \left\lbrace\begin{array}{rll} x &= 2, &(1)^\prime = (1) - (2)^\prime\cr y &= 3. &(2)^\prime \end{array}\right. \end{array} \] と式変形していたが, 行列を用いて表現した際にも, 第 $2$ 行に第 $1$ 行の $-2$ 倍を加える, といった操作で同じ変形を表すことができる: \[ \begin{array}{rl} & \begin{pmatrix} 1&1\cr 2&3 \end{pmatrix}\begin{pmatrix} x\cr y \end{pmatrix} = \begin{pmatrix} 5\cr 13 \end{pmatrix} \cr \leadsto & \begin{pmatrix} 1&1\cr 0&1 \end{pmatrix}\begin{pmatrix} x\cr y \end{pmatrix} = \begin{pmatrix} 5\cr 3 \end{pmatrix} \cr \leadsto & \begin{pmatrix} 1&0 \cr 0&1 \end{pmatrix}\begin{pmatrix} x\cr y \end{pmatrix} = \begin{pmatrix} 2\cr 3 \end{pmatrix}. \end{array} \] 行列に対するこのような操作は基本変形と呼ばれるものであり, この例のように連立 $1$ 次方程式の解の計算 (このような計算方法を掃き出し法 もしくは ガウスの消去法という) など, 様々な応用を持つものである.
行列 $A$ が \[ A = \begin{pmatrix} 1&1 \cr 2&3 \end{pmatrix} \] という形をしている時は, 上で見たようにこの行列 $A$ を基本変形により単位行列に変形することができる (これにより $A\mathbf{x} = \mathbf{b}$ の解 $\mathbf{x}$ はただ一つに定まる). 実は, ある行列を基本変形で単位行列に変形できることと, その行列が正則である (つまり逆行列を持つ) こととは同値である (これは階数という概念を用いて説明される). もっと言えば, ある行列を単位行列にする基本変形は逆行列と同一視できるため, 掃き出し法は逆行列の計算方法として用いることもできる.
この章では, 行列の基本変形と呼ばれる特定の変形, 及びこれに関連する基本行列の性質について解説し, またそれらの応用として連立 $1$ 次方程式を解く, すなわち逆行列を計算する手順について紹介する. コンピュータシミュレーションなどへの応用の際には, 巨大な行列を用いて表される連立 $1$ 次方程式を考えることになるが, ここでは手計算が可能な程度の規模, つまりサイズの小さい行列のみ具体例として取り上げることにする.
2.2: 基本変形
行列に対する基本的な操作として, 以下の $3$ つを行基本変形 (elementary row operations) という:
- 第 $i$ 行と第 $j$ 行を入れ替える.
- 第 $i$ 行に $0$ でない数を掛ける.
- 第 $i$ 行に第 $j$ 行のスカラー倍を加える.
また, 以下の $3$ つを列基本変形 (elementary column operations) という:
- 第 $i$ 列と第 $j$ 列を入れ替える.
- 第 $i$ 列に $0$ でない数を掛ける.
- 第 $i$ 列に第 $j$ 列のスカラー倍を加える.
ただし, $i\neq j$ とする.
例えば, $A=\begin{pmatrix} a & b \cr c & d \end{pmatrix}$ に対する行基本変形は,
- $\begin{pmatrix} a & b \cr c & d \end{pmatrix} \longrightarrow \begin{pmatrix} c & d \cr a & b \end{pmatrix},$
- $\begin{pmatrix} a & b \cr c & d \end{pmatrix} \longrightarrow \begin{pmatrix} a & b \cr \lambda c & \lambda d \end{pmatrix},$
- $\begin{pmatrix} a & b \cr c & d \end{pmatrix} \longrightarrow \begin{pmatrix} a & b \cr \lambda a + c & \lambda b + d \end{pmatrix},$
といったものである.
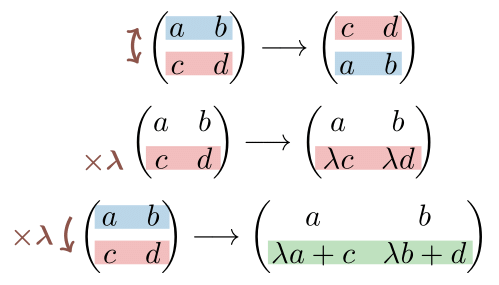
行列に対する基本変形は, 以下に挙げる行列を掛けることにより表現することができる.
以下の $3$ つの正方行列を基本行列 (elementary matrix) という:
- $P_{i,j}$: 単位行列 $I$ の 第 $i$ 行と第 $j$ 行を入れ替えたもの.
- $Q_{i,\lambda}$: 単位行列 $I$ の $(i,i)$ 成分を $\lambda\neq0$ に置き換えたもの.
- $R_{i,j,\lambda}$: 単位行列 $I$ の $(i,j)$ 成分を $\lambda$ に置き換えたもの.
- 行列 $A$ に対する行基本変形は, $A$ に基本行列を左から掛けることで表現できる.
- 行列 $A$ に対する列基本変形は, $A$ に基本行列を右から掛けることで表現できる.
\[ A = \begin{pmatrix} a & b\cr c & d \end{pmatrix}. \]
- $P_{1,2} = \begin{pmatrix} 0 & 1 \cr 1 & 0 \end{pmatrix}$ であり, \[ \begin{array}{rl} P_{1,2}A &= \begin{pmatrix} 0 & 1 \cr 1 & 0 \end{pmatrix}\begin{pmatrix} a & b \cr c & d \end{pmatrix} \cr & = \begin{pmatrix} c & d \cr a & b \end{pmatrix}. \end{array} \] この行列は, 行列 $A$ に「第 $1$ 行と第 $2$ 行を入れ替える」という行基本変形を適用したものに等しい.
- $Q_{2,\lambda} = \begin{pmatrix} 1 & 0 \cr 0 & \lambda \end{pmatrix}$ であり, \[ \begin{array}{rl} Q_{2,\lambda}A &= \begin{pmatrix} 1 & 0 \cr 0 & \lambda \end{pmatrix}\begin{pmatrix} a & b \cr c & d \end{pmatrix} \cr & = \begin{pmatrix} a & b \cr \lambda c & \lambda d \end{pmatrix}. \end{array} \] この行列は, 行列 $A$ に「第 $2$ 行に $\lambda$ を掛ける」という行基本変形を適用したものに等しい.
- $R_{2,1,\lambda} = \begin{pmatrix} 1 & 0 \cr \lambda & 1 \end{pmatrix}$ であり, \[ \begin{array}{rl} R_{2,1,\lambda}A &= \begin{pmatrix} 1 & 0 \cr \lambda & 1 \end{pmatrix}\begin{pmatrix} a & b \cr c & d \end{pmatrix} \cr & = \begin{pmatrix} a & b \cr \lambda a + c & \lambda b + d \end{pmatrix}. \end{array} \] この行列は, 行列 $A$ に「第 $2$ 行に第 $1$ 行の $\lambda$ 倍を加える」という行基本変形を適用したものに等しい.
つまり, 行基本変形は
- 行列 $A$ に左から $P_{i,j}$ を掛ける ($A$ を $P_{i,j}A$ に置き換える),
- 行列 $A$ に左から $Q_{i, \lambda}$ を掛ける ($A$ を $Q_{i,\lambda}A$ に置き換える), ただし $\lambda\neq0$ とする,
- 行列 $A$ に左から $R_{i,j,\lambda}$ を掛ける ($A$ を $R_{i,j,\lambda}A$ に置き換える)
という操作であると表現することができる. また, 例えば行列 $A$ に「第 $i$ 行と第 $j$ 行を入れ換える」という行基本変形を適用した行列に, さらに「第 $i$ 行を $\lambda$ 倍する」という行基本変形を適用したものは, \[ Q_{i,\lambda}(P_{i,j}A) = Q_{i,\lambda}P_{i,j}A \] と一致する (行列積の順番に注意).
基本行列は全て正則行列であり, \[ P_{i,j}^{-1}=P_{i,j}, \] \[ Q_{i,\lambda}^{-1} = Q_{i,\lambda^{-1}}, \] \[ R_{i,j,\lambda}^{-1} = R_{i,j,-\lambda} \] となる, すなわち, 基本行列の逆行列は基本行列である. 実際, 例えば \[ P_{i,j}P_{i,j} = P_{i,j}P_{i,j}I \] は, 単位行列 $I$ に「第 $i$ 行と第 $j$ 行を入れ換える」という行基本変形を適用した行列に, さらに「第 $i$ 行と第 $j$ 行を入れ換える」という行基本変形を適用したものであり, これは単位行列 $I$ になる. つまり \[ P_{i,j}P_{i,j} = I \] であり, 従って $P_{i,j}^{-1} = P_{i,j}$ である. $Q_{i,\lambda}^{-1} = Q_{i,\lambda^{-1}}$ および $R_{i,j,\lambda}^{-1} = R_{i,j,-\lambda}$ も同様に確かめることができる.
2.3: 階数と正則性
基本行列を用いて, 与えられた行列 $A$ を, 基本行列と"簡単な形をした行列"の積により \[ A = (\text{基本行列たちの積})\widetilde{A}(\text{基本行列たちの積}) \] と表現することを考える. これは, 行列 $A$ に対する基本変形により, "簡単な形をした行列" $\widetilde{A}$ を得ることを意味している.
まず, 基本変形の性質を用いることで, 以下が成立する:
行列 $A=(a_{ij})$ の $(p,q)$ 成分が $0$ でないなら, 基本変形により第 $p$ 行 及び第 $q$ 列の成分を, $(p,q)$ 成分のみ $1$, それ以外を全て $0$ にすることができる (これを第 $p$ 行および第 $q$ 列を掃き出すという).
- まず, 第 $p$ 行を $a_{pq}$ で割ることで, $(p,q)$ 成分を $1$ にすることができる.
- 次に, $p$ 以外の全ての $i$ に対し, 第 $p$ 行の $(i,q)$ 成分倍を引くことで, 第 $q$ 列は $(p,q)$ 成分を除いて全て $0$ になる.
- 最後に, 第 $q$ 列に対して同様の操作を行うことで, 第 $q$ 列は $(p,q)$ 成分を除いて全て $0$ になる.
\[ A = \begin{pmatrix} 2&4&6\cr 2&3&4\cr 1&3&5 \end{pmatrix}. \]
- この行列の第 $1$ 行と第 $1$ 列を掃き出してみよう.
- つまり 第 $1$ 行と 第 $1$ 列について, $(1,1)$ 成分のみ $1$, それ以外は $0$ とする基本変形を考える.
- まず, 第 $1$ 行を $a_{11}=2$ で割ることで $(1,1)$ 成分を $1$ にする: \[ Q_{1,1/2}A = \begin{pmatrix} 1&2&3\cr 2&3&4\cr 1&3&5 \end{pmatrix}. \]
- 次に, 第 $2$ 行に第 $1$ 行の $-2$ 倍を加え, 第 $3$ 行に第 $1$ 行の $-1$ 倍を加える, これにより, 第 $1$ 列は $(1,1)$ 成分を除いて全て $0$ になる: \[ R_{3,1,-1}R_{2,1,-2}Q_{1,1/2}A = \begin{pmatrix} 1&2&3\cr 0&-1&-2\cr 0&1&2 \end{pmatrix}. \] 記号の簡単のため, $\widetilde{P} = R_{3,1,-1}R_{2,1,-2}Q_{1,1/2}$ とおく.
- 最後に, 第 $2$ 列に第 $1$ 列の $-2$ 倍を加え, 第 $3$ 列に第 $1$ 列の $-3$ 倍を加える, これにより, 第 $1$ 行は $(1,1)$ 成分を除いて全て $0$ になる: \[ \widetilde{P}AR_{2,1,-2}R_{3,1,-3} = \begin{pmatrix} 1&0&0\cr 0&-1&-2\cr 0&1&2 \end{pmatrix}. \] 記号の簡単のため, $\widetilde{Q} = R_{2,1,-2}R_{3,1,-3}$ とおく.
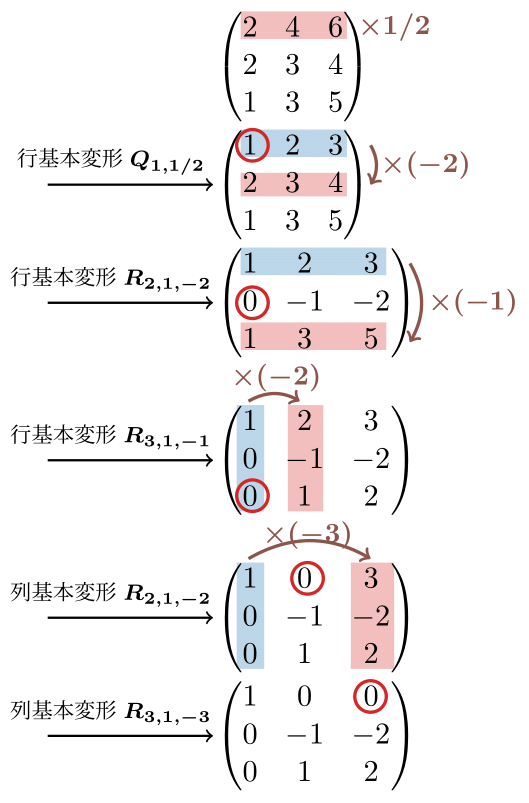
上の例では, 行列 $A$ の $(1,1)$ 成分に注目して掃き出しを行うことで, 第 $1$ 行と第 $1$ 列を $(1,1)$ 成分のみ $1$ に, それ以外を $0$ にすることができた. 同様に, $(2,2)$ 成分に注目して掃き出しを行うことで $(2,2)$ 成分のみを $1$ に, それ以外を $0$ にすることができると期待される. この手順を繰り返し, $i=1,2,\dots$ について, 行列 $A$ の第 $(i,i)$ 成分に注目した掃き出しを行うことで, $A$ を基本変形により単位行列に"近づける"ことができる. つまり, \[ A = (\text{基本行列たちの積})\widetilde{A}(\text{基本行列たちの積}) \] を満たす $\widetilde{A}$ として, 単位行列に似た行列を求めることができる.
\[ A = \begin{pmatrix} 2&4&6\cr 2&3&4\cr 1&3&5 \end{pmatrix}. \]
- この行列の第 $1$ 行と第 $1$ 列を掃き出すと (上の例より), \[ \widetilde{A} = \widetilde{P}A\widetilde{Q} = \begin{pmatrix} 1 & 0 & 0 \cr 0 & -1 & -2 \cr 0 & 1 & 2 \end{pmatrix} \] と変形することができる.
- このようにして得られた行列について, さらに第 $2$ 行と第 $2$ 列を掃き出してみよう.
- まず, 第 $2$ 行を $\widetilde{a}_{22}=-1$ で割ることで $(2,2)$ 成分を $1$ にする: \[ Q_{2,-1}\widetilde{A} = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 2 \cr 0 & 1 & 2 \end{pmatrix}. \]
- 次に, 第 $3$ 行に第 $2$ 行の $-1$ 倍を加える, これにより, 第 $2$ 列は $(2,2)$ 成分を除いて全て $0$ になる: \[ R_{3,2,-1}Q_{2,-1}\widetilde{A} = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 2\cr 0 & 0 & 0 \end{pmatrix}. \]
- 最後に, 第 $3$ 列に第 $2$ 列の $-2$ 倍を加える, これにより, 第 $2$ 行は $(2,2)$ 成分を除いて全て $0$ になる: \[ R_{3,2,-1}Q_{2,-1}\widetilde{A}R_{3,2,-2} = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 0 \end{pmatrix}. \]
- 記号の簡単のため, 改めて \[ \widetilde{P} = R_{3,2,-1}Q_{2,-1}R_{3,1,-1}R_{2,1,-2}Q_{1,1/2}, \] \[ \widetilde{Q} = R_{2,1,-2}R_{3,1,-3}R_{3,2,-2} \] とおくと, \[ \widetilde{P}A\widetilde{Q} = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 0 \end{pmatrix} \] が得られたことになる.
どのような行列に対しても, 基本変形により上と同様の"単位行列に似た行列"を得ることがが可能である. このことは, 階数という言葉を用いて以下のように言及される:
任意の行列 $m\times n$ 型行列 $A$ は, 基本変形により $m\times n$ 型行列 \[ F(r) =\begin{pmatrix} I_r&O\cr O&O \end{pmatrix} = \begin{pmatrix} 1\cr &1\cr &&\ddots\cr &&&1\cr &&&&0\cr &&&&&\ddots \end{pmatrix} \] に変形できる, ここで $I_r$ は $r\times r$ 型の単位行列である (ブロック行列を用いて表現している).
言い換えれば, 基本行列の積により表される行列 $P$, $Q$ を用いて, $A=PF(r)Q$ と表すことができる.
この $r$ を行列 $A$ の階数(rank)という.
- $A=O$ ならば, $A=F(0)$ なので成立.
- $A\neq O$ ならば, $0$ でない成分があるため, 基本変形 (行及び列の入れ替え) によりその成分を 第 $1$ 行, 第 $1$ 列 に移動させる.
- 上の補題より, 第 $1$ 行及び第 $1$ 列を, $(1,1)$ 成分のみ $1$ に, それ以外を $0$ にするような基本変形が存在する: \[ P^\prime AQ^\prime = \left(\begin{array}{cc} 1&O\cr O&A^\prime \end{array}\right) \]
- $A^\prime=O$ なら $P^\prime AQ^\prime = F(1)$, そうでなければ $0$ でない成分を第 $2$ 行, 第 $2$ 列に移動させ, 同様の操作により \[ P^{\prime\prime} A Q^{\prime\prime} = \left(\begin{array}{cc} I_2&O\cr O&A^{\prime\prime}\end{array}\right) \] が得られる.
- この手順を繰り返すことにより, 最終的に \[ \widetilde{P} A \widetilde{Q} = F(r) \] という形が得られる, ただし $\widetilde{P}$, $\widetilde{Q}$ は基本行列の積で表される.
- 基本行列は正則であり, 逆行列も基本行列で表される. ここで, (正則行列の積が正則行列であることから $\widetilde{P}$, $\widetilde{Q}$ も正則行列なので) $P=\widetilde{P}^{-1}$, $Q=\widetilde{Q}^{-1}$ とすれば, $P$, $Q$ は基本行列の積で表され, \[ A = P\widetilde{P}A\widetilde{Q}Q = PF(r)Q \] が成立する.
- 行列 $A$ の階数が $r$ であるとき, $\operatorname{rank} A = r$ と表記する.
- 行列 $F(r)$ を, 行列 $A$ の標準形と呼ぶことがある.
- 本当は, このような $r$ が一意に定まることも示す必要があるが, ここでは証明は省略する.
上の定理について, 特に行列 $A$ が $n$ 次正方行列である場合に注目する. 行列 $A$ に基本変形を行なった場合に得られる "簡単な形をした行列" は, 上の結果より
- 単位行列 $I$ に一致する ( $\operatorname{rank}A = n$ の場合に相当する), もしくは
- 単位行列 $I$ のいくつかの対角成分を $0$ に取り替えたものに一致する ( $\operatorname{rank}A \lt n$ の場合に相当する)
のいずれかであることがわかる.
実は正方行列の階数と正則性 (すなわち逆行列の存在) とは密接に関連している: 具体的には, $n$ 次正方行列 $A$ が逆行列を持つことと $\operatorname{rank}A = n$ であること (標準形が単位行列であること) は同値である. つまり正則行列は基本変形により単位行列にできる、一方で正則でない行列は基本変形により単位行列にできない:
$A$ を $n$ 次正方行列とする. このとき, 以下が成立する:
- $\operatorname{rank}A = n \iff A \text{ は正則}.$
- $\operatorname{rank}A \lt n \iff A \text{ は正則でない}.$
- 上の定理より, $A=PF(r)Q$ と表すことができるのであった, ただし $P$, $Q$ は基本行列の積で表される行列であり, $r=\operatorname{rank}A$に対し $F(r)\in\mathbb{R}^{n\times n}$ は \[ F(r) = \begin{pmatrix} I_r&O\cr O&O \end{pmatrix} \] という形の行列である. $P$, $Q$ は正則なので, \[ A \text{ が正則} \iff F(r)\text{ が正則} \] が得られる. 従って, $r = \operatorname{rank}A$ について, \[ r=n \iff F(r) \text{ が正則} \] を示せば良い:
- $(\implies)$ $r=\operatorname{rank}A=n$ ならば, $F(r)$ は $n$ 次の単位行列となるため特に正則である.
- $(\impliedby)$ 対偶を示す: $r\lt n$ のとき, $F(r)$ が正則でないことを示せば良い.
(背理法) $F(r)$ が正則であると仮定する, このとき $F(r)^{-1}$ が存在し $F(r)F(r)^{-1}=I$ となる. 一方で $r \lt n$ なので, $F(r)$ の 第 $r+1$ 行から第 $n$ 行の成分は全て $0$ である. 従って, $F(r)F(r)^{-1}$ の第 $r+1$ 行から第 $n$ 行の成分も全て $0$ となるため, $F(r)F(r)^{-1}\neq I$ となり矛盾する.
- 以上より \[ \operatorname{rank} A=n \iff F(r) \text{ が正則} \] が証明される.
- $m\times n$ 型行列 $A$ について, $\operatorname{rank}A=\min\lbrace m,n\rbrace$ のとき, $A$ はフルランク (full rank) であるということがある.
- 特に $A$ が正方行列のときは, $A$ がフルランクならば対応する標準形 $F(r)$ は単位行列になり, 従って逆行列を持つ: \[ \text{正方行列 } A \text{ がフルランク}\iff A \text{ が正則} \]
上の結果より, 正方行列 $A$ が正則ならば基本行列の積 $P$, $Q$ を用いて \[ A = PIQ = PQ \] と表すことができる. 従って以下が成立する:
$A$ を $n$ 次正方行列とする. このとき, 以下が成立する: \[ A\text{ が正則}\iff A\text{ は基本行列の積で表現される}. \]
さらに, 基本行列たちの積 $P$, $Q$ を用いて $A=PQ$ と表されるとき, \[ Q^{-1}P^{-1}A = Q^{-1}P^{-1}PQ = I \] が得られる. 基本行列の逆行列は基本行列となるため, $Q^{-1}P^{-1}$ も基本行列の積である. これと, 行列 $A$ に左から基本行列を掛けることは $A$ に行基本変形を行うことを意味していることから, 以下のように言い換えることもできる:
$A$ を $n$ 次正方行列とする. このとき, 以下が成立する: \[ A\text{ が正則} \iff A \text{ は行基本変形だけで単位行列にできる} \]
ある行列 $A$ を行基本変形だけで単位行列にできるかどうかを確かめる際に, どのような手順で行基本変形を適用しても構わない (結果は変わらない). ここでは具体的な計算手順として, 各対角成分に対する掃き出しのうち, 行基本変形の部分のみを行うことを推奨する. つまり, $i=1, 2, \dots$ に対して,
- 必要ならば第 $i$ 行とそれ以降の行の入れ替えを行う, 少なくとも $(i,i)$ 成分を非ゼロにする必要がある.
- 第 $i$ 行を $(i,i)$ 成分 ($\neq0$) で割ることで, $(i,i)$ 成分を $1$ にする,
- 行基本変形により, 第 $i$ 列を $(i,i)$ 成分を除いて全て $0$ にする
という手順で計算することを推奨する.
\[ A = \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix},\quad B= \begin{pmatrix} -2&1\cr 3/2&-1/2 \end{pmatrix}. \] このとき, $AB=BA=I$ なので $A^{-1}=B$ である, つまり $A$ は正則行列である. この行列 $A$ が行基本変形のみで単位行列に変形できることを確かめてみよう.
以降, 行基本変形を矢印 ($\longrightarrow$) で表すことにする: \[ \begin{array}{rll}A =& \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix} \quad & \left(\text{$a_{11}=1$ なので変形不要}\right) \cr \longrightarrow&\begin{pmatrix} 1&2\cr 0&-2 \end{pmatrix} \quad &\left(\begin{array}{c}\text{第 $2$ 行に第 $1$ 行の}\cr \text{$-3$ 倍を加えた}\end{array}\right)\cr \longrightarrow&\begin{pmatrix} 1&2\cr 0&1 \end{pmatrix} \quad &\left(\begin{array}{c}\text{第 $2$ 行を $-1/2$ 倍して}\cr \text{$a_{22}=1$ に変形}\end{array}\right)\cr \longrightarrow&\begin{pmatrix} 1&0\cr 0&1 \end{pmatrix} \quad &\left(\begin{array}{c}\text{第 $1$ 行に第 $2$ 行の}\cr \text{$-2$ 倍を加えた}\end{array}\right) \end{array} \] これは基本行列を左から掛けて表現すると, $R_{1,2,-2}Q_{2,-1/2}R_{2,1,-3}A = I$ となることを意味している.
ここまでの内容を改めて整理すると,
- 全ての行列は, 行基本変形に加えて 列基本変形も用いると, 標準形 $F(r)$ に変形できる (単位行列も標準形のひとつである),
- 行列 $A$ が正則 $\iff$ 行列 $A$ は 行基本変形だけで単位行列 $I$ に変形できる,
- 行列 $A$ が正則でない $\iff$ 行列 $A$ は行基本変形で単位行列 $I$ に変形することはできない
となる. 全ての正則でない行列は, 行基本変形に加えて 列基本変形も用いることで 標準形 $F(r)$ に変形できるが, それは単位行列ではない.
さて, 正則でない行列を, 行基本変形だけで (単位行列にすることができないのは上述の通りだが) 標準形にすることができるかというと, 一般には否である.
\[ C = \begin{pmatrix} 1&2\cr 2&4 \end{pmatrix}. \] この行列は逆行列を持たない. この行列に行基本変形を行うと, \[ \begin{array}{rll}C =& \begin{pmatrix} 1&2\cr 2&4 \end{pmatrix}\quad&\cr \longrightarrow& \begin{pmatrix} 1&2\cr 0&0 \end{pmatrix} \quad &\left(\begin{array}{c}\text{第 $2$ 行に第 $1$ 行の}\cr \text{$-2$ 倍を加えた}\end{array}\right) \end{array} \] などとなる. これ以上行基本変形を行なっても, 標準形にすることはできない.
なお, 行基本変形だけでなく, 列基本変形も用いると, $ \begin{pmatrix} 1&0\cr 0&0 \end{pmatrix}$ という標準形にすることができるが, これは単位行列ではない.
このように, 正則でない行列 (正方行列でない行列も含む) に対して 行基本変形のみ 施した場合, 一般には標準形にすることはできない. ただし, 実は行簡約階段形 (reduced row echelon form) という形にすることができることが知られている. 行簡約階段形とは何かを説明するために, まずは主成分 (leading coefficient) を紹介する:
行列の各行に対して, $0$ でない成分のうち最も左にあるものを主成分 (leading coefficient) という.
行列 $A=\begin{pmatrix} 1 & 2 & 3 & 4 \cr 0 & 0 & 5 & 6 \cr 0 & 0 & 0 & 0 \end{pmatrix}$ について,
- 第 $1$ 行の主成分は $(1,1)$ 成分の $1$ である,
- 第 $2$ 行の主成分は $(2,3)$ 成分の $5$ である,
- 第 $3$ 行は主成分を持たない.
以下を満たす行列を 行階段形 (row echelon form) であるという:
- ① 全ての成分が $0$ となる行が, そうでない行より下にある,
- ② 各行の主成分は (存在するなら), その行より上にある他の行の主成分よりも右側にある.
さらに, 追加で以下を満たす行列を 行簡約階段形 (reduced row echelon form) であるという:
- ③ 全ての主成分が $1$ である,
- ④ 主成分を含む列の他の成分が全て $0$ である.
- 行列 $A=\begin{pmatrix} 1 & 2 & 3 & 4 \cr 0 & 0 & 5 & 6 \cr 0 & 0 & 0 & 0 \end{pmatrix}$ は行階段形ではあるが, $1$ でない主成分が存在するため行簡約階段形ではない.
- 行列 $B=\begin{pmatrix} 1 & 2 & 3 & 4 \cr 0 & 0 & 1 & 6/5 \cr 0 & 0 & 0 & 0 \end{pmatrix}$ は行階段形ではあるが, 第 $2$ 行の主成分を含む列 (第 $3$ 列) に, 主成分でも $0$ でもない成分が存在するため行簡約階段形ではない.
- 行列 $C=\begin{pmatrix} 1 & 2 & 0 & 2/5 \cr 0 & 0 & 1 & 6/5 \cr 0 & 0 & 0 & 0 \end{pmatrix}$ は行簡約階段形である.
- 上に挙げた行列について, 行列 $A$ を行基本変形で $B$ に, さらに $B$ を行基本変形により $C$ に変形できることが確認できる. つまり, 行簡約階段形でない行列に行基本変形を行うことで, 行簡約階段形の条件が満たされるように変形することができる.
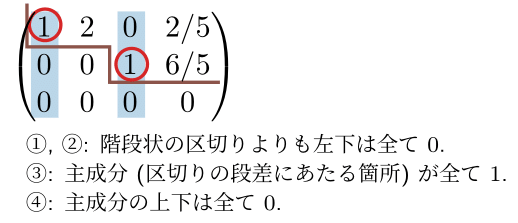
行列 $A$ に対して, 行基本変形により得られる行簡約階段形はただ一つに定まり, 行基本変形の順序には依存しない. 具体的な計算手順としては, 正則行列を単位行列に変形する手順と同様の手順を推奨する. 具体的には, $i = 1, 2, \dots, n$ の順に,
- 必要ならば第 $i$ 行とそれ以降の行の入れ替えを行い, 少なくとも ① が, 可能な限り ② が満たされるようにする,
- 第 $i$ 行を第 $i$ 行の主成分 ($\neq0$) で割ることで, ③ が満たされるようにする,
- 行基本変形により, 第 $i$ 行の主成分が含まれる列を, 主成分を除いて全て $0$ にする (④ が満たされるようにする)
という手順で計算することを推奨する.
行簡約階段形が得られれば, あとは列基本変形により標準形 $F(r)$ に変形することができる. このとき, $0$ でない成分を含む行は, 列基本変形を用いても $\mathbf{0}$ にはできない.
このことは, 以下のように言い換えることもできる:
ここで, 単位行列も行簡約階段形の一種であることに注意して, 上にまとめた内容を書き直しておく:
- 全ての行列は, 行基本変形だけで行簡約階段形に変形できる,
- 特に, 行列 $A$ が正則 $\iff$ 行列 $A$ は行基本変形だけで単位行列 $I$ に変形できる,
- 行列 $A$ が正則でない $\iff$ 行列 $A$ は行基本変形で行簡約階段形には変形できるが, それは単位行列 $I$ ではない.
- ある行列に対して標準形を求めるためには (一般には) 列基本変形も用いる必要があるが, 階数を求めるだけならば行基本変形だけで良い.
2.4: 掃き出し法 (ガウスの消去法)
上述のように, 行列に対して行基本変形を行うことで, 行簡約階段形 (単位行列を含む) に変形することができる. このような計算手順 (アルゴリズム) を掃き出し法 (row reduction) もしくは ガウスの消去法 (Gaussian elimination) という.
掃き出し法は, 先ほども紹介したように, 行列の階数を求めるテクニックとして応用できるが, 他にも連立 $1$ 次方程式の解法, もしくは逆行列を計算する方法としても応用することができる. これらを説明するため, まず拡大行列という概念を導入する.
行の数が等しい $2$ つの行列 $A$, $B$ に対して, それらを横に連結して得られる行列 $\left(\begin{array}{c:c}A&B\end{array}\right)$ を拡大行列 (augmented matrix) という.
拡大行列は, $2$ つの行列に同じ行基本変形を行う際に, 記述を簡単にするために用いられる.
\[A = \begin{pmatrix} 1&2&3\cr 2&3&4\cr 1&3&5 \end{pmatrix},\quad I = \begin{pmatrix} 1&0&0\cr 0&1&0\cr 0&0&1 \end{pmatrix},\quad \mathbf{b} = \begin{pmatrix} 4\cr 7\cr 5 \end{pmatrix}.\] このとき, \[ \left(\begin{array}{c:c}A&I\end{array}\right) = \left(\begin{array}{ccc:ccc} 1&2&3&1&0&0\cr 2&3&4&0&1&0\cr 1&3&5&0&0&1 \end{array}\right), \]\[ \left(\begin{array}{c:c}A&\mathbf{b}\end{array}\right) = \left(\begin{array}{ccc:c} 1&2&3&4\cr 2&3&4&7\cr 1&3&5&5 \end{array}\right). \]
まず, 掃き出し法による逆行列の計算方法を紹介する.
例えば \[ \begin{array}{rll}A =& \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix} \quad & \left(\text{$a_{11}=1$ なので変形不要}\right) \cr \longrightarrow&\begin{pmatrix} 1&2\cr 0&-2 \end{pmatrix} \quad &\left(\begin{array}{c}\text{第 $2$ 行に第 $1$ 行の}\cr \text{$-3$ 倍を加えた}\end{array}\right)\cr \longrightarrow&\begin{pmatrix} 1&2\cr 0&1 \end{pmatrix} \quad &\left(\begin{array}{c}\text{第 $2$ 行を $-1/2$ 倍して}\cr \text{$a_{22}=1$ に変形}\end{array}\right)\cr \longrightarrow&\begin{pmatrix} 1&0\cr 0&1 \end{pmatrix} \quad &\left(\begin{array}{c}\text{第 $1$ 行に第 $2$ 行の}\cr \text{$-2$ 倍を加えた}\end{array}\right) \end{array} \] という行基本変形は, 基本行列を用いて表記すると \[ R_{1,2,-2}Q_{2,-1/2}R_{2,1,-3}A = I \] と同じことを意味しているのだった. これは \[ \begin{array}{rl} A^{-1} &= R_{1,2,-2}Q_{2,-1/2}R_{2,1,-3} \cr &= R_{1,2,-2}Q_{2,-1/2}R_{2,1,-3}I \end{array} \] ということに他ならない. 言い換えると, 次が成立する:
行列 $A$ を行基本変形で単位行列に変形することができるならば, 同じ行基本変形を単位行列 $I$ に対して適用することで $A^{-1}$ を得ることができる.
これによる逆行列の計算を, 拡大行列を用いて記述してみよう: \[ \begin{array}{rll}\left(\begin{array}{c:c}A&I\end{array}\right) =& \left(\begin{array}{cc:cc} 1&2&1&0\cr 3&4&0&1 \end{array}\right)\cr \longrightarrow&\left(\begin{array}{cc:cc} 1&2&1&0\cr 0&-2&-3&1 \end{array}\right) \quad &\left(\begin{array}{c}\text{第 $2$ 行に第 $1$ 行の}\cr \text{$-3$ 倍を加えた}\end{array}\right)\cr \longrightarrow&\left(\begin{array}{cc:cc} 1&2&1&0\cr 0&1&3/2&-1/2 \end{array}\right) \quad &\text{(第 $2$ 行を $-1/2$ 倍した)}\cr \longrightarrow&\left(\begin{array}{cc:cc} 1&0&-2&1\cr 0&1&3/2&-1/2 \end{array}\right) \quad &\left(\begin{array}{c}\text{第 $1$ 行に第 $2$ 行の}\cr \text{$-2$ 倍を加えた}\end{array}\right) \end{array} \] このように, 拡大行列 $\left(\begin{array}{c:c}A&I\end{array}\right)$ に対して行基本変形を行うことで, 行列 $A$ と単位行列 $I$ に対して同じ行基本変形を適用できる. 定理より, 左側を単位行列に変形することができたので, 右側が $A^{-1}$ となる.
この計算による結果は行基本変形の順序に依存しない. 具体的な計算手順としては, 拡大行列の左側 $A$ にやはり正則行列を単位行列に変形する手順をそのまま適用することを推奨する. つまり, $i = 1, 2, \dots, n$ の順に,
- 必要ならば第 $i$ 行とそれ以降の行の入れ替えを行う, 少なくとも $(i,i)$ 成分を非ゼロにする必要がある.
- 第 $i$ 行を $(i,i)$ 成分 ($\neq0$) で割ることで, $(i,i)$ 成分を $1$ にする,
- 行基本変形により, 第 $i$ 列を $(i,i)$ 成分を除いて全て $0$ にする
という手順で計算することを推奨する.
もしも $A$ が正則行列でなかったならば, 拡大行列 $\left(\begin{array}{c:c}A&I\end{array}\right)$ に対する行基本変形により左側を単位行列に変形することはできない. このことを利用すれば, $A$ が正則であるかどうかの判定も行うことができる.
次に, 掃き出し法を用いて連立 $1$ 次方程式を解く方法を紹介する.
例として次を考えよう: \[ \left\lbrace\begin{array}{rll} x+2y &= 20, &(1)\cr 3x+4y &= 46. &(2) \end{array}\right. \] この連立 $1$ 次方程式を行列を用いて \[ A\mathbf{x} = \mathbf{b} \] と表記できる, ここで \[ A = \begin{pmatrix} 1&2\cr 3&4 \end{pmatrix}, \quad \mathbf{x}=\begin{pmatrix} x\cr y \end{pmatrix}, \quad \mathbf{b} = \begin{pmatrix} 20\cr 46 \end{pmatrix}. \] もしも $A$ が正則行列であるならば, $\mathbf{x} = A^{-1}A\mathbf{x} = A^{-1}\mathbf{b}$ を計算することで連立 $1$ 次方程式の解 $x$, $y$ を得ることができる. 先ほども見たように $A^{-1}$ は (存在するならば) 行列 $A$ を単位行列にする行基本変形により表現できる. 言い換えれば, 次が成立する:
行列 $A$ を行基本変形で単位行列に変形することができるならば, 同じ行基本変形を列ベクトル$\mathbf{b}$に対して行うことで $A^{-1}\mathbf{b}$ を得ることができる.
上に例として挙げた連立 $1$ 次方程式 $A\mathbf{x}=\mathbf{b}$ を掃き出し法により解いて $\mathbf{x} = A^{-1}\mathbf{b}$ を求めてみよう:
\[ \begin{array}{rll}\left(\begin{array}{c:c}A&\mathbf{b}\end{array}\right) =& \left(\begin{array}{cc:c} 1&2&20\cr 3&4&46 \end{array}\right)\cr \longrightarrow&\left(\begin{array}{cc:c} 1&2&20\cr 0&-2&-14 \end{array}\right) \quad &\left(\begin{array}{c}\text{第 $2$ 行に第 $1$ 行の}\cr \text{$-3$ 倍を加えた}\end{array}\right)\cr \longrightarrow&\left(\begin{array}{cc:c} 1&2&20\cr 0&1&7 \end{array}\right) \quad &\text{(第 $2$ 行を $-1/2$ 倍した)}\cr \longrightarrow&\left(\begin{array}{cc:c} 1&0&6\cr 0&1&7 \end{array}\right) \quad &\left(\begin{array}{c}\text{第 $1$ 行に第 $2$ 行の}\cr \text{$-2$ 倍を加えた}\end{array}\right).\end{array} \]このように, 拡大行列 $\left(\begin{array}{c:c}A&\mathbf{b}\end{array}\right)$ に対する行基本変形により, 左側を単位行列に変形することができたならば, 右側が $A^{-1}\mathbf{b}$ となるため, これが連立 $1$ 次方程式の解 $\mathbf{x}$ である.
もしも $A$ が正則行列でなかったならば (正方行列でない場合も含む), 拡大行列 $\left(\begin{array}{c:c}A&\mathbf{b}\end{array}\right)$ に対する行基本変形により左側を単位行列に変形することはできない. これは, 連立 $1$ 次方程式の解が存在しない, もしくは一意に定まらないことを意味する.
\[ \left\lbrace\begin{array}{rll} x+2y &= a, &(1)\cr 2x+4y &= b. &(2) \end{array}\right. \] という連立 $1$ 次方程式, もしくはこれと行列を用いて表記した \[ \begin{pmatrix} 1&2\cr 2&4 \end{pmatrix} \begin{pmatrix} x\cr y \end{pmatrix} = \begin{pmatrix} a\cr b \end{pmatrix} \] を考える. 拡大行列に対する掃き出し法により \[ \left(\begin{array}{cc:c} 1&2&a\cr 2&4&b \end{array}\right)\longrightarrow \left(\begin{array}{cc:c} 1&2&a\cr 0&0&b-2a \end{array}\right) \] と, 左側を行簡約階段形にすることができるが, 左側を単位行列にすることはできない. この行階段形は, \[ \left\lbrace\begin{array}{rll} x+2y &= a, &(1)\cr 0x+0y &= b-2a. &(2)^{\prime} \end{array}\right. \] と同値であるが, この問題は $b-2a\neq 0$ ならば解は存在しない. 一方で, $b-2a=0$ ならば $x+2y=a$ を満たす全ての $x$, $y$ が解となる.
上の例のように, 実は $A$ が正則でない場合には $A\mathbf{x}=\mathbf{b}$ という問題の解 $\mathbf{x}$ は存在しないか, もしくはある条件を満たすもの全てが解になるかのいずれかになる. 一方, $A$ が正則ならば $\mathbf{x} = A^{-1}\mathbf{b}$ がただ一つの解となる. つまり, 連立 $1$ 次方程式 $A\mathbf{x}=\mathbf{b}$ の解は,
- ($A$ が正則であって) ただ一つ存在する,
- ($A$ が正則ではなく) 存在しない,
- ($A$ が正則ではなく) ある条件を満たす $\mathbf{x}$ が全て解となる
のいずれかとなる. いま, $A\mathbf{x}=\mathbf{0}$ という問題は必ず解 $\mathbf{x}=\mathbf{0}$ を持つので, この問題の解はただ一つ (つまり $\mathbf{x}=\mathbf{0}$ のみが解) であるか, もしくはある条件を満たす $\mathbf{x}$ 全てが解となるかのいずれかとなる.
行列 $A$ と列ベクトル $\mathbf{x}$ に対し, $A\mathbf{x} = \mathbf{0}$ という形の式を斉次連立 $1$ 次方程式という.
もう一度書いておくと, 斉次連立 $1$ 次方程式について, $\mathbf{x}=\mathbf{0}$ が解となることは簡単にわかる (これを自明な解という). 上で述べたように, 正方行列 $A$ が正則であれば, 解は $\mathbf{x} = A^{-1}\mathbf{0} = \mathbf{0}$ 以外には存在しない. 一方で, 正方行列 $A$ が正則でない場合には, 実はある条件を満たす $\mathbf{x}$ 全てが解となる: 特に, 必ず $\mathbf{x} = \mathbf{0}$ 以外の解 (非自明な解) が存在する (このことの厳密な証明は4: 線型結合で述べる). この対偶を考えると, 斉次連立 $1$ 次方程式が非自明な解を持たないならば, $A$ は正則行列である.
このことを定理としてまとめておく:
$n$ 次正方行列 $A$ についての斉次連立 $1$ 次方程式 $A\mathbf{x}=\mathbf{0}$ について, 以下が成立する:
\[ A \text{が正則} \iff \text{非自明な解は存在しない.} \]\[ \begin{pmatrix} 1&2\cr 2&4 \end{pmatrix} \begin{pmatrix} x\cr y \end{pmatrix} = \begin{pmatrix} 0\cr 0 \end{pmatrix} \] を考える. 拡大行列に対する掃き出し法により \[ \left(\begin{array}{cc:c} 1&2&0\cr 0&0&0 \end{array}\right) \] という行簡約階段形が得られるが, この第 $2$ 行は \[ 0\cdot x+0\cdot y = 0 \] を意味しており矛盾しない. 従って, 第 $1$ 行が意味する \[ x + 2y = 0 \] を満たす全ての $x$, $y$ が解となる. これは,
\[ A \text{が正則でない} \implies \text{非自明な解が存在する} \] の具体例となっている.まとめ
基本変形および基本行列について紹介し, これらに関連して階数と掃き出し法 (ガウスの消去法) について解説した.
特に, $n$ 次正方行列 $A$ に対して, 階数 $\operatorname{rank}A$ が $n$ であること (つまり基本変形で単位行列にできること) が, $A$ が正則行列である (逆行列 $A^{-1}$ が存在する) ことの必要十分条件であることを示した. また, このことから任意の正則行列は基本行列の積であり, 従って任意の正則行列 $A$ の逆行列 $A^{-1}$ は, $A$ を単位行列にする基本変形により表されることがわかる. これを利用して逆行列を計算する, もしくは連立 $1$ 次方程式を解く方法として掃き出し法 (ガウスの消去法) を紹介した.
基本行列の性質は 3: 行列式 において再び用いることになり, また行列の階数は行列の特徴を表す基本的なアイデアであり, 以降も関連する話題が現れる. これらの概念はこの資料全体の内容と複雑に関連するものであり, よくわからないからと放置すると, 以降の説明の理解に支障が出るだろう. 先に進む前に, このページの内容をよく確認することを勧める. また掃き出し法 (ガウスの消去法) における具体的な計算手順も, 基本行列や階数について理解する助けとなるだろう.
練習問題
\[ A = \begin{pmatrix} 5 & -5 & 2 & 16 \cr 0 & 1 & 2 & 4 \cr 10 & -10 & 5 & 35 \end{pmatrix} \] とする.
- この行列 $A$ を行基本変形により行簡約階段形に変形せよ.
- 行列 $A$ の階数を求めよ.
$a$, $b$ を実数とする. このとき, \[ A = \begin{pmatrix} 1 & a \cr b & 1 \end{pmatrix} \] の階数を求めよ. また, 行列 $A$ を正則にする $a$, $b$ を求めよ.
$a$, $b$, $c$, $d$, $e$, $f\in\mathbb{R}$ に対し, \[ A = \begin{pmatrix} a & 0 & 0 \cr d & b & 0 \cr e & f & c \end{pmatrix} \] とする, ただし $abc\neq0$ とする. このとき, $A^{-1}$ を求めよ.
次の連立 $1$ 次方程式を解け: \[ \begin{pmatrix} 5 & 1 & 1 \cr 1 & -1 & 4 \cr 1 & 5 & -1 \end{pmatrix}\begin{pmatrix} x \cr y \cr z \end{pmatrix} = \begin{pmatrix} -11 \cr 0 \cr -25 \end{pmatrix}. \]