補足: 平面の線形変換
A.1: 表現行列
ベクトル $\mathbf{v}$ をベクトル $\mathbf{w}$ に移す写像 $f$ を考える, つまり \[ \mathbf{w} = f(\mathbf{v}) \] とする. 本来であれば, より抽象的にベクトル空間を導入するところから始めるべきであろうが, ここではベクトルとして列ベクトル (およびそれと同一視できる幾何ベクトル) のみを考える. このとき, 写像 $f$ のことを関数と呼ぶことがある.
写像 (関数) $f$ が次の性質を満たすとき, $f$ を線形変換 (linear transform) もしくは線形写像 (linear mapping), 線形関数 (linear function) という:
- 任意の $\mathbf{v}_1$, $\mathbf{v}_2$ に対し, \[ f(\mathbf{v}_1+\mathbf{v}_2) = f(\mathbf{v}_1) + f(\mathbf{v}_2). \]
- 任意のベクトル $\mathbf{v}$ と任意のスカラー値 $\lambda$ に対し, \[ f(\lambda\mathbf{v}) = \lambda f(\mathbf{v}). \]
特に, 任意のベクトルを $\mathbf{0}$ に移す変換は線形変換である. このような線形変換を零写像という.
いま, "行列を列ベクトルの左から掛ける"という操作はこの性質を満たすので, ある行列 $A$ を用いて \[ f(\mathbf{v}) = A\mathbf{v} \] と表すことができる写像 $f$ は線形変換である.
ところで, 行列を用いて表すことができないような線形変換が存在するかというと, 答えは否である. つまり, ベクトルをベクトルに移す任意の線形変換 $f$ に対して, 必ず対応する行列 $A$ が存在し $f(\mathbf{v}) = A\mathbf{v}$ が成り立つ.
このことを (大雑把にではあるが) 解説する: まず, 任意のベクトル $\mathbf{v}\in\mathbb{R}^m$ に対して, $f(\mathbf{v})\in\mathbb{R}^n$ であるとする. いま, 任意のベクトル $\mathbf{v}\in\mathbb{R}^m$ は線型結合を用いて \[ \mathbf{v} = \begin{pmatrix} v_1\cr v_2\cr \vdots\cr v_m \end{pmatrix} = v_1\mathbf{e}_1 + v_2\mathbf{e}_2 + \dots + v_m\mathbf{e}_m \] と表すことができる, ここで $\mathbf{e}_j\in\mathbb{R}^m$ は標準基底である.
さて, 写像 $f$ の線形性を用いると \[ \begin{array}{rl} f(\mathbf{v}) &= f(v_1\mathbf{e}_1 + v_2\mathbf{e}_2 + \dots + v_m\mathbf{e}_m) \cr &= f(v_1\mathbf{e}_1) + f(v_2\mathbf{e}_2) + \dots + f(v_m\mathbf{e}_m) \cr &= v_1f(\mathbf{e}_1) + v_2f(\mathbf{e}_2) + \dots + v_mf(\mathbf{e}_m) \cr &= \begin{pmatrix}f(\mathbf{e}_1), f(\mathbf{e}_2), \dots, f(\mathbf{e}_m)\end{pmatrix}\mathbf{v} \end{array} \] が成り立つ, ここで $f(\mathbf{e}_j) \in\mathbb{R}^n$ は列ベクトルであり, $f(\mathbf{e}_j)$ を第 $j$ 列ベクトルに持つ行列 \[ \begin{pmatrix}f(\mathbf{e}_1), f(\mathbf{e}_2), \dots, f(\mathbf{e}_m)\end{pmatrix} \] は $n\times m$ 型行列である. そこで, この行列を $A$ とおくと, \[ f(\mathbf{v}) = \begin{pmatrix}f(\mathbf{e}_1), f(\mathbf{e}_2), \dots, f(\mathbf{e}_m)\end{pmatrix}\mathbf{v} = A\mathbf{v} \] が得られるのである. このように, ベクトルをベクトルに移す線形変換は行列と同一視することができる. 線形変換と同一視される行列 $A$ を表現行列という.
一般には, 表現行列は各ベクトル空間に指定した基底に応じて定まるものであるが, 上では標準基底を用いた場合のみ考えている. 異なる基底を用いた場合には, 同じ線形変換 $f$ に対する表現行列であっても異なるものになるが, ここでは深入りしない.
線形変換は, 幾何ベクトルを幾何ベクトルに移す変換とみることで, 図形的な解釈が可能であるが, その前に線形変換の性質をいくつか確認しておく.
まず, $2$ つの線形変換 $f$, $g$ に対し, これらの和 $h = f+g$ を, \[ h(\mathbf{v}) = f(\mathbf{v}) + g(\mathbf{v}) \] と定めると, $h$ も線形変換となる. また, $f$ の表現行列を $A$, $g$ の表現行列を $B$ とおくと, $h=f+g$ の表現行列は $A+B$ となる.
次に, $2$ つの線形変換 $f$, $g$ に対し, これらの合成 $h = f\circ g$ を, \[ h(\mathbf{v}) = f(g(\mathbf{v})) \] と定めると, $h$ も線形変換となる. また, $f$ の表現行列を $A$, $g$ の表現行列を $B$ とおくと, $h=f\circ g$ の表現行列は $AB$ となる.
最後に逆変換を紹介する. 線形変換 $f$ の表現行列は (標準基底を用いた場合) \[ A = \begin{pmatrix}f(\mathbf{e}_1), f(\mathbf{e}_2), \dots, f(\mathbf{e}_m)\end{pmatrix} \in \mathbb{R}^{n\times m} \] と表すことができ, このとき $f(\mathbf{v}) = A\mathbf{v}$ となるのだった. もしもこの表現行列 $A$ が正則ならば, $g(\mathbf{v}) = A^{-1}\mathbf{v}$ という線形変換は, \[ f(g(\mathbf{v})) = \mathbf{v},\quad g(f(\mathbf{v})) = \mathbf{v} \] を満たす. この性質を満たす線形変換 $g$ を $f$ の逆変換という. 逆変換を持つ線形変換 (つまり表現行列が正則である線形変換) は可逆であるという.
A.2: アフィン変換
以降, 簡単のため $2\times 1$ 型の列ベクトル $\mathbf{x}$ に対する変換のみを考えることにする. いま, このベクトル $\mathbf{x}$ は, $xy$ 平面上の点と同一視することができる. これを用いると, $xy$ 平面上の図形は, ある性質を満たすベクトル $\mathbf{x}$ たちの集合として表すことができる.
さて, $xy$ 平面上の図形は $\mathbb{R}^2$ の部分集合として記述することが可能である. 特に, 図形に対する線形変換を考える際には, しばしば以下のような図形を用いる: \[ \Delta^n = \left\{(x_1,\dots, x_n)\in\mathbb{R}^n \mid x_1,\dots,x_n \gt 0,\ \displaystyle\sum_{i=1}^nx_i \lt 1\right\}. \] このような図形 $\Delta^n\subset\mathbb{R}^n$ を標準単体 (standard simplex) もしくは 単位単体 (unit simplex) という.
$n=2$ の場合は, $\Delta^2$ は $xy$ 平面上の $3$ つの直線 $x=0$, $y=0$, $x+y=1$ で囲まれる部分であり, つまり \[ \mathbf{0} = \begin{pmatrix} 0 \cr 0 \end{pmatrix},\quad \mathbf{e}_1 = \begin{pmatrix} 1 \cr 0 \end{pmatrix},\quad \mathbf{e}_2 = \begin{pmatrix} 0 \cr 1 \end{pmatrix} \] を頂点とする直角 $2$ 等辺三角形の内部となる. また, \[ \Delta^2 = \left\{c_1\mathbf{e}_1 + c_2\mathbf{e}_2\in\mathbb{R}^2 \mid c_1, c_2\gt 0,\ c_1+c_2\lt 1\right\} \] と表すことができる.
次に, このような図形に対する変換の一例として, アフィン変換を紹介する.
簡単のため, $n=2$ の場合を考える. ある図形を表す集合 $K\subset\mathbb{R}^2$ について, $\mathbf{x}\in K$ を アフィン変換により移したものを考えてみる: \[ K' = \{f(\mathbf{x})\in\mathbb{R}^2 \mid \mathbf{x}\in K\} \] この $K'$ も $xy$ 平面上の図形を表しているとみなせるため, これによりアフィン変換は『図形を図形に移す』変換であるとみなすことができる.
例えば, 以下の変形は全てアフィン変換により表現することができる.
- 回転: \[ \begin{pmatrix} \cos\varphi & -\sin\varphi \cr \sin\varphi & \cos\varphi \end{pmatrix}\begin{pmatrix} r\cos\theta\cr r\sin\theta \end{pmatrix} = \begin{pmatrix} r\cos(\theta+\varphi) \cr r\sin(\theta+\varphi) \end{pmatrix}. \]
- 拡大, 縮小: \[ \begin{pmatrix} \alpha & 0 \cr 0 & \beta \end{pmatrix}\begin{pmatrix} x \cr y \end{pmatrix} = \begin{pmatrix} \alpha x \cr \beta y \end{pmatrix}. \]
- せん断 (例えば長方形を平行四辺形にするように, 傾きを加える変換): \[ \begin{pmatrix} 1 & \gamma \cr 0 & 1 \end{pmatrix}\begin{pmatrix} x \cr y \end{pmatrix} = \begin{pmatrix} x + \gamma y \cr y \end{pmatrix}, \text{ もしくは } \] \[ \begin{pmatrix} 1 & 0 \cr \gamma & 1 \end{pmatrix}\begin{pmatrix} x \cr y \end{pmatrix} = \begin{pmatrix} x \cr \gamma x + y \end{pmatrix} \]
- 並行移動: \[ \begin{pmatrix} x \cr y \end{pmatrix} + \begin{pmatrix} b_1 \cr b_2 \end{pmatrix} = \begin{pmatrix} x+b_1 \cr y+b_2 \end{pmatrix}. \]
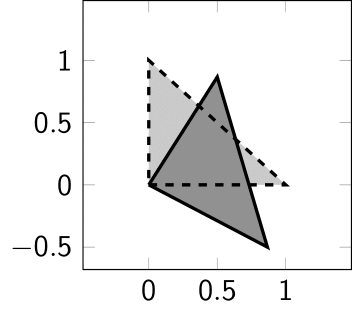
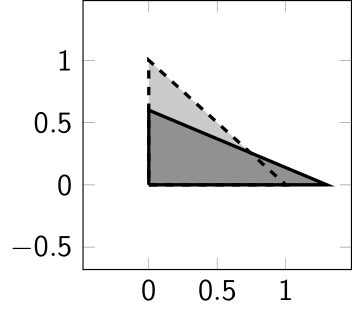
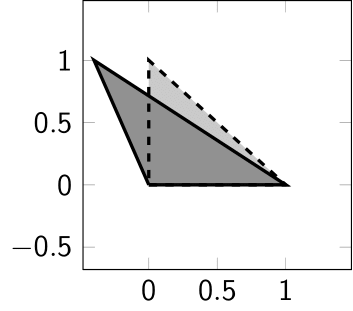
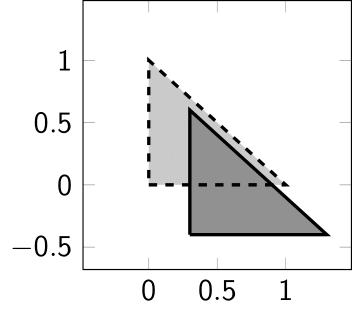
いま, 簡単のため $n=2$ の場合に \[ \mathbf{x} = \begin{pmatrix} x_1 \cr x_2 \end{pmatrix},\quad f(\mathbf{x}) = \begin{pmatrix} f_1 \cr f_2 \end{pmatrix},\quad A = \begin{pmatrix} a_{11} & a_{12} \cr a_{21} & a_{22} \end{pmatrix},\quad \mathbf{b} = \begin{pmatrix} b_1 \cr b_2 \end{pmatrix} \] と表記する. このとき, アフィン変換は \[ \begin{pmatrix} f_1 \cr f_2 \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} \cr a_{21} & a_{22} \end{pmatrix}\begin{pmatrix} x_1 \cr x_2 \end{pmatrix} + \begin{pmatrix} b_1 \cr b_2 \end{pmatrix} \] と表されるが, これは以下と同値となる: \[ \begin{pmatrix} f_1 \cr f_2 \cr 1 \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & b_1 \cr a_{21} & a_{22} & b_2 \cr 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x_1 \cr x_2 \cr 1 \end{pmatrix}. \] このように, アフィン変換は行列の形で表現することができ, 従ってアフィン変換の合成は, 対応する行列の積を計算することにより表現することができる. 画像処理などに用いられる複雑な変形であっても, それがアフィン変換の合成により表すことができるならば, 行列の計算に帰着させることができるのである.
A.3: 正則行列の図形的解釈
簡単のため, 上で紹介したアフィン変換から並行移動を除いた \[ f(\mathbf{x}) = A\mathbf{x} \qquad (\mathbf{x}\in\mathbb{R}^n,\ A\in\mathbb{R}^{n\times n}) \] を考えてみよう. これは『図形を図形に写す』と解釈することができるのだった. 以降, 線形変換 $f$ と行列 $A$ とを同一視し, 『行列 $A$ により図形を図形に移す』などと表現することにする.
標準単体 $\Delta^2$ を線形変換 $f$ で移した図形は, $f$ の線形性に注意すると \[ \left\{c_1f(\mathbf{e}_1) + c_2f(\mathbf{e}_2)\in\mathbb{R}^2 \mid c_1,c_2\gt 0,\ c_1+c_2\lt 1\right\} \] と表される. これは, \[ \mathbf{0},\quad f(\mathbf{e}_1),\quad f(\mathbf{e}_2) \] を頂点とする三角形の内部となる.
$n$ 次元球体の内部は \[ \left\{x_1\mathbf{e}_1 + x_2\mathbf{e}_2 + \dots + x_n\mathbf{e}_n \in\mathbb{R}^n \mid \displaystyle\sum_{i=1}^n x_i^2 \lt 1\right\} \] と表され, これを線形変換 $f$ で移した図形は \[ \left\{x_1f(\mathbf{e}_1) + x_2f(\mathbf{e}_2) + \dots + x_nf(\mathbf{e}_n)\in \mathbb{R}^n \mid \displaystyle\sum_{i=1}^n x_i^2 \lt 1\right\} \] となる.
ここで, 行列 $A$ が正則であるか否かにより, 『図形を図形に移す』操作にどのような違いがあるかを考えてみよう. 標準基底を用いることで, \[ A = (f(\mathbf{e}_1), f(\mathbf{e}_2), \dots, f(\mathbf{e}_n)) \] と表すことができるが, ここで正方行列 $A$ が正則であることは, $f(\mathbf{e}_1)$, $f(\mathbf{e}_2)$, $\dots$, $f(\mathbf{e}_m)$ が線型独立であることと同値である (正則性の必要十分条件). 例えば, $n=2$ の場合を考えると, \[ f(\mathbf{e}_1) = cf(\mathbf{e}_2) \] となっていれば (つまりベクトル $f(\mathbf{e}_1)$ と $f(\mathbf{e}_2)$ が同じ向きを持つならば) $f(\mathbf{e}_1), f(\mathbf{e}_2)$ は線型独立ではない. このとき, 標準単体 $\Delta^2$ を移した図形は, \[ \mathbf{0},\quad f(\mathbf{e}_1),\quad f(\mathbf{e}_2) \] の $3$ 点をつなぐと線分となってしまい, 三角形にならない. 直感的には, 標準単体のような図形を移した時に "潰してしまう" 行列は正則ではない. 逆に, 図形を "潰さない" 行列は正則行列である.
上の説明に基づき, 正方行列に対する 正則性の必要十分条件 に対する図形的な解釈を (数学的に厳密なものではないが) 解説する.
\[ A = \begin{pmatrix} 1 & 2 \cr 3 & 4 \end{pmatrix},\quad B = \begin{pmatrix} 1 & 2 \cr 2 & 4 \end{pmatrix}. \] いま, 行列 $A$ は正則であるが, 行列 $B$ は正則ではない. 実際に, 標準基底 $\mathbf{e}_1$, $\mathbf{e}_2$ を (つまり 標準単体 $\Delta^2$ を) 行列 $A$, $B$ で移したものを以下に図示する:
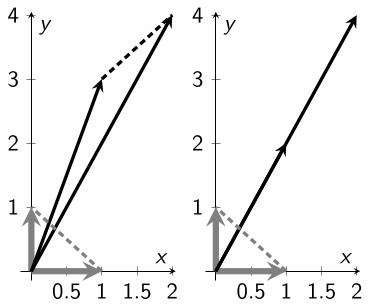
行列 $A$ による線形変換で標準基底を移したベクトルが線型独立でない場合, この線形変換は図形を "潰してしまう" ことになり, 変形前の図形の情報が失われてしまう (元の図形を復元することができなくなってしまう). これは, 線形変換が可逆ではない (逆行列が存在しない) ことを意味しており, \[ A \text{ が正則} \iff A\text{ の列ベクトルが線型独立} \] に対応している.
いま, 標準単体 $\Delta^2$ を行列 \[ A = \begin{pmatrix} a & b \cr c & d \end{pmatrix} \] で移した図形は, \[ \mathbf{0},\quad \mathbf{a} = \begin{pmatrix} a \cr c \end{pmatrix},\quad \mathbf{b} = \begin{pmatrix} b \cr d \end{pmatrix} \] を頂点とする三角形となる. 標準単体 $\Delta^2$ の面積は $1/2$ だが, この三角形の面積は (幾何ベクトル $\vec{a}$, $\vec{b}$ と列ベクトル $\mathbf{a}$, $\mathbf{b}$ を同一視して表記すると) \[ \begin{array}{rl} \dfrac{1}{2}\sqrt{|\mathbf{a}|^2|\mathbf{b}|^2 - (\mathbf{a}\cdot\mathbf{b})^2} &= \dfrac{1}{2}\sqrt{(a^2+c^2)(b^2+d^2) - (ab+cd)^2} \cr &= \dfrac{1}{2}|ad-bc| \end{array} \] となり, つまり標準単体の面積の $|\det A|$ 倍である. もしも $\det A=0$ ならば, 標準単体を行列 $A$ で移した図形の面積は $0$ であり, これは $A$ による線形変換は図形を潰してしまうことを意味している. このことは, \[ A\text{ が正則} \iff \det A\neq 0 \] に対応している.
上と同じ行列で, 円盤 \[ \left\{x\mathbf{e}_1 + y\mathbf{e}_2\in\mathbb{R}^2 \mid x^2+y^2 \lt 1\right\} \] を移した図形を以下に図示する:
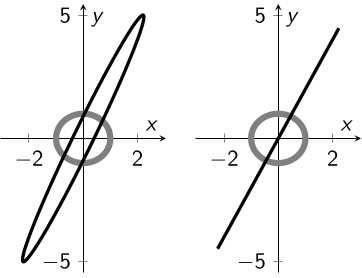
正則行列による線形変換では, $\mathbf{0}$ 以外の点を $\mathbf{0}$ に移すことがない (逆に, 正則でない行列は, $\mathbf{0}$ 以外の点を $\mathbf{0}$ に集中させることで図形を潰している). このことは, \[ A \text{ が正則} \iff A\mathbf{x} = \mathbf{0} \text{ が非自明な解を持たない} \] に対応している.
行列 \[ A = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \end{pmatrix},\quad B = \begin{pmatrix} 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 1 & 0 \end{pmatrix},\quad C = \begin{pmatrix} 1 & 0 & 0 \cr 1 & 0 & 0 \cr 1 & 0 & 0 \end{pmatrix} \] とする. このとき, $\operatorname{rank}A = 3$, $\operatorname{rank}B = 2$, $\operatorname{rank}C = 1$ である. これらの行列で, 球 \[ \left\{x\mathbf{e}_1 + y\mathbf{e}_2 + z\mathbf{e}_3\in\mathbb{R}^3 \mid x^2+y^2+z^2 \lt 1\right\} \] を移した図形を以下に図示する:
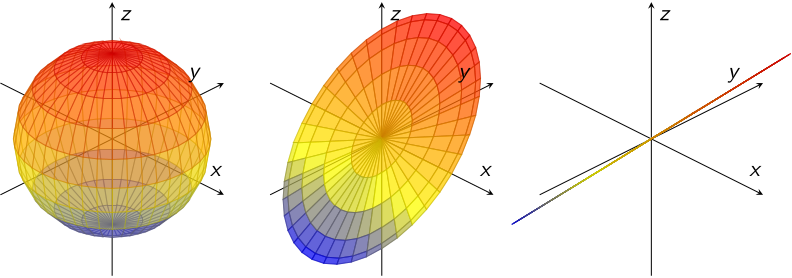
球は行列 $B$ により平面となり, 行列 $C$ により線になる (いずれも体積が $0$ であることが, $\det B=\det C=0$ に対応している). 元の図形は $3$ 次元の立体としての情報を持っていたが, 行列 $B$ により $2$ 次元の図形となり (つまり $1$ 次元分の情報を失い), 行列 $C$ により $1$ 次元の図形となっている ($2$ 次元分の情報を失っている). このように, 行列の階数は『その行列による線形変換がどれだけの次元の情報を維持できるか』を表しているとみなすことができる. $1$ つでも次元の情報を失う (このことを退化すると言うことがある) と図形は潰れてしまうため, フルランクでない行列は正則ではない. このことが, $n$ 次正方行列 $A$ に対して \[ A\text{ が正則} \iff \operatorname{rank}A = n \] に対応している.